The nonlinear ear
/Hearing, audition, or audioception, is one of the Famous Five of our twenty or so senses. Indeed, it is the most powerful sense, having about 100 dB of dynamic range, compared to about 90 dB for vision. Like vision, hearing — which is to say, the ear–brain system — has a nonlinear response to stimuli. This means that increasing the stimulus by, say, 10%, does not necessarily increase the response by 10%. Instead, it depends on the power and bandwidth of the signal, and on the response of the system itself.
What difference does it make if hearing is nonlinear? Well, nonlinear perception produces some interesting effects. Some of them are especially interesting to us because hearing is analogous to the detection of seismic signals — which are just very low frequency sounds, after all.
Stochastic resonance (Zeng et al, 2000)
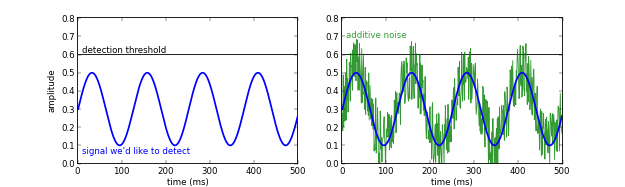
One of the most unintuitive properties of nonlinear detection systems is that, under some circumstances, most importantly in the presence of a detection threshold, adding noise increases the signal-to-noise ratio.
I'll just let you read that last sentence again.
Add noise to increase S:N? It might seem bizarre, and downright wrong, but it's actually a fairly simple idea. If a signal is below the detection threshold, then adding a small Goldilocks amount of noise can make the signal 'peep' above the threshold, allowing it to be detected. Like this:
I have long wondered what sort of nonlinear detection system in geophysics might benefit from a small amount of noise. It also occurs to me that signal reconstruction methods like compressive sensing might help estimate that 'hidden' signal from the few semi-random samples that peep above the threshold. If you know of experiments in this, I'd love to hear about it.
Better than Heisenberg (Oppenheim & Magnasco, 2012)
Denis Gabor realized in 1946 that Heisenberg's uncertainty principle also applies to linear measures of a signal's time and frequency. That is, methods like the short-time Fourier transform (STFT) cannot provide the time and the frequency of a signal with arbitrary precision. Mathematically, the product of the uncertainties has some minimum, sometimes called the Fourier limit of the time–bandwidth product.
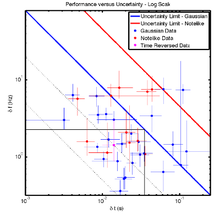 So far so good. But it turns out our hearing doesn't work like this. It turns out we can do better — about ten times better.
So far so good. But it turns out our hearing doesn't work like this. It turns out we can do better — about ten times better.
Oppenheim & Magnasco (2012) asked subjects to discriminate the timing and pitch of short sound pulses, overlapping in time and/or frequency. Most people were able to localize the pulses, especially in time, better than the Fourier limit. Unsurprisingly, musicians were especially sensitive, improving on the STFT by a factor of about 10. While seismic signals are not anything like pure tones, it's clear that human hearing does better than one of our workhorse algorithms.
Isolating weak signals (Gomez et al, 2014)
One of the most remarkable characteristics of biological systems is adaptation. It seems likely that the time–frequency localization ability most of us have is a long-term adaption. But it turns out our hearing system can also rapidly adapt itself to tune in to specific types of sound.
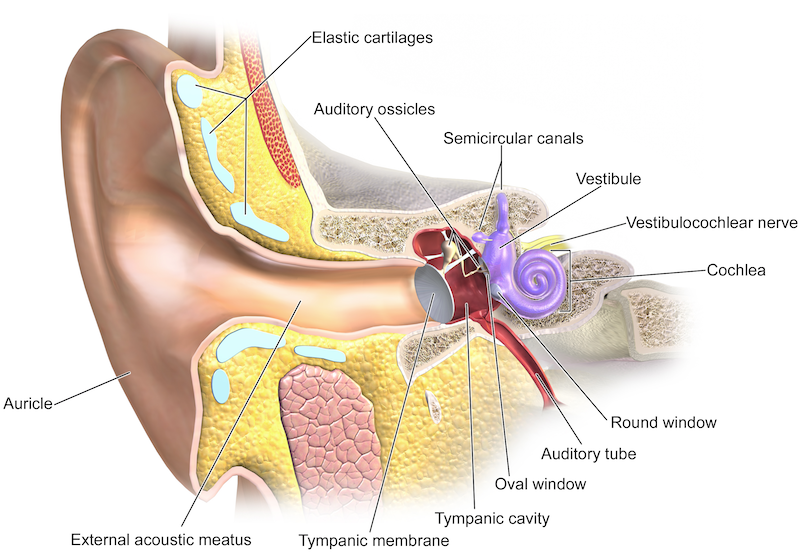 Listening to a voice in a noisy crowd, or a particular instrument in an orchestra, is often surprisingly easy. A group at the University of Zurich has figured out part of how we do this. Surprisingly, it's not high-level processing in the auditory cortex. It's not in the brain at all; it's in the ear itself.
Listening to a voice in a noisy crowd, or a particular instrument in an orchestra, is often surprisingly easy. A group at the University of Zurich has figured out part of how we do this. Surprisingly, it's not high-level processing in the auditory cortex. It's not in the brain at all; it's in the ear itself.
That hearing is an active process was known. But the team modeled the cochlea (right, purple) with a feature called Hopf bifurcation, which helps describe certain types of nonlinear oscillator. They established a mechanism for the way the inner ear's tiny mechanoreceptive hairs engage in active sensing.
What does all this mean for geophysics?
I have yet to hear of any biomimetic geophysical research, but it's hard to believe that there are no leads here for us. Are there applications for stochastic resonance in acquisition systems? We strive to make receivers with linear responses, but maybe we shouldn't! Could our hearing do a better job of time-frequency localization than any spectral decomposition scheme? Could turning seismic into music help us detect weak signals in the geological noise?
All very intriguing, but of course no detection system is perfect... you can fool your ears too!
References
Zeng FG, Fu Q, Morse R (2000). Human hearing enhanced by noise. Brain Research 869, 251–255.
Oppenheim, J, and M Magnasco (2013). Human time-frequency acuity beats the Fourier uncertainty principle. Physical Review Letters. DOI 10.1103/PhysRevLett.110.044301 and in the arXiv.
Gomez, F, V Saase, N Buchheim, and R Stoop (2014). How the ear tunes in to sounds: A physics approach. Physics Review Applied 1, 014003. DOI 10.1103/PhysRevApplied.1.014003.
The stochastic resonance figure is original, inspired by Simonotto et al (1997), Physical Review Letters 78 (6). The figure from Oppenheim & Magnasco is copyright of the authors. The ear image is licensed CC-BY by Bruce Blaus.
This story about exploiting stochastic resonance for improving balance in the elderly just came up on my radar. And, BTW, IEEE Spectrum is a great amagzine... highly recommended.








 Except where noted, this content is licensed
Except where noted, this content is licensed