Species identification in the rock kingdom
/Like geology, life is studied across a range of scales. Plants and animals come in a bewildering diversity of shapes and sizes. Insects can be microscopic, like fleas, or massive, like horned beetles; redwood trees tower 100 metres tall, and miniature alpine plants fit into a thimble.
In biology, there is an underlying dynamic operating on all organisms that constrain the dimensions and mass of each species. These constraints, or allometric scaling laws, play out everywhere on earth because of the nature and physics of water molecules. The surface tension of water governs the strength of a cell wall, and this in turn mandates the maximum height and width of a body, any possible body.
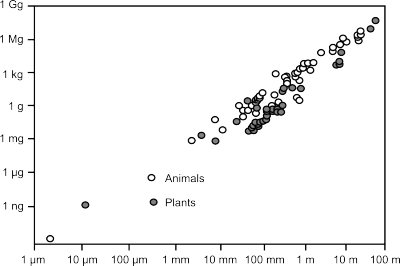
← The relationship between an organisms size and mass. Click the image to read Kevin Kelly's fascinating take on this subject.
Amazingly, both animal and plant life forms adhere to a steady slope of mass per unit length. Life, rather than being boundless and unlimited in every direction, is bounded and limited in many directions by the nature of matter itself. A few things caught my attention when I saw this graph. If your eye is keenly tuned, you'll see that plants plot in a slightly different space than animals, with the exception of only a few outliers that cause overlap. Even in the elegantly constructed world of the biological kingdom, there are deviations from nature's constraints. Scientists looking at raw data like these might certainly describe the outliers as "noise", but I don't think that's correct in this case; it's just undescribed signal. If this graphical view of the biological kingdom is used as a species identifcation challenge, sometimes a plant can 'look' like an animal, but it really isn't. It's a plant. A type II error may be lurking.
Finally, notice the wishbone pattern in the data. It's reminded me of some Castagna-like trends I have come across in the physics of rocks, and I wonder if this suggests a common end-member source of some kind. I won't dare to elaborate on these patterns in the animal kingdom or plant kingdom, but it's what I strive for in the rock kingdom.
I wonder if this example can serve as an analog for many rock physics relationships, whereby the fundamental properties are governed by some basic building blocks. Life forms have carbon and DNA as their common roots, whereas sedimentary rocks don't necessarily have ubiquitous building blocks; some rocks can be rich in silica, some rocks can have none at all.
← Gardner's equation: the relationship between acoustic velocity and bulk density for sedimentary rocks. Redrawn from Gardner et al (1974).
For comparison, look at this classic figure from Gardner et al in which they deduced an empirical relationship between seismic P-wave velocity and bulk density. As in the first example, believing that all species fall on this one global average (dotted line) is cursory at best. But, that is exactly what Gardner's equation describes. In fact, it fits more closely to high-velocity dolomites than it does for the sands and silts for which it is typically applied. Here, I think we are seeing the constraints from water impose themselves differently on the formation of different minerals, and depositional elements. Deviations from the global average are meaningful, and density estimation and log editing techniques should (and usually do) take these shifts into account. Even though this figure doesn't have any hard data on it, I am sure you could imagine that, just as with biology, crossovers and clustering would obscure these relatively linear deductions.

← The mudrock line: relationship between shear velocity and compressional velocitiy, modfified from Castagna et al (1985).
The divergence of mudrocks from gas sands that John Castagna et al discovered seems strikingly similar to the divergence seen between plant and animal cells. Even the trend lines suggest a common or indistinguishable end member. Certainly the density and local kinetic energy of moving water has alot to do with the deposition and architecture of sediment bodies. The chemical and physical properties of water affect sediments undergoing burial and compaction, control diagensis, and control pore-fluid interactions. Just as water is the underlying force causing the convergence in biology, water is one (and perhaps not the only) driving force that constrains the physical properties of sedimentary rocks. Any attempts at regression and cluster analyses should be approached with these observations in mind.
References
Kelly, K (2010). What Technology Wants. New York, Viking Penguin.
Gardner, G, L Gardner and A Gregory (1974). Formation velocity and density—the diagnostic basics for stratigraphic traps. Geophysics 39, 770–780.
Castagna, J, M Batzle and R Eastwood (1985). Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics 50, 571–581.
Evan's post today is the 100th post on Agile*, exactly 222 days after the first. Tomorrow we will highlight one or two of our favourite posts since we started last November.









 Except where noted, this content is licensed
Except where noted, this content is licensed