The power of stack
/Multiplicity is a basic principle of seismic acquisition. Our goal is to acquite lots of traces—lots of spatial samples—with plenty of redundancy. We can then exploit the redundancy, by mixing traces, sacrificing some spatial resolution for increased signal:noise. When we add two traces, the repeatable signal adds constructively, reinforcing and clarifying. The noise, on the other hand, is spread evenly about zero and close to random, and tends to cancel itself. This is why you sometimes hear geophysicists refer to 'the power of stack'.
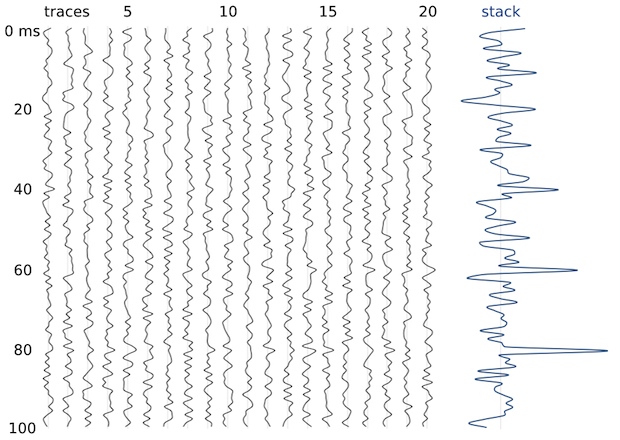 Here's an example. There are 20 'traces' of 100-digit-long sequences of random numbers (white noise). The numbers range between –1 and +1. I added some signal to samples 20, 40, 60 and 80. The signals have amplitude 0.25, 0.5, 0.75, and 1. You can't see them in the traces, because these tiny amplitudes are completely hidden by noise. The stacked trace on the right is the sum of the 20 noisy traces. We see mostly noise, but the signal emerges. A signal of just 0.5—half the peak amplitude of the noise—is resolved by this stack of 20 traces; the 0.75 signal stands out beautifully.
Here's an example. There are 20 'traces' of 100-digit-long sequences of random numbers (white noise). The numbers range between –1 and +1. I added some signal to samples 20, 40, 60 and 80. The signals have amplitude 0.25, 0.5, 0.75, and 1. You can't see them in the traces, because these tiny amplitudes are completely hidden by noise. The stacked trace on the right is the sum of the 20 noisy traces. We see mostly noise, but the signal emerges. A signal of just 0.5—half the peak amplitude of the noise—is resolved by this stack of 20 traces; the 0.75 signal stands out beautifully.
 Here's another example, but with real data. This is part of Figure 3 from Liu, G, S Fomel, L Jin, and X Chen (2009). Stacking seismic data using local correlation. Geophysics 74 (2) V43–V48. On the left is an NMO-corrected (flattened) common mid-point gather from a 2D synthetic model with Gaussian noise added. These 12 traces each came from a single receiver, though in this synthetic case the receiver was a virtual one. Now we can add the 12 traces to get a single trace, which has much stronger signal, relative to the background noise, than any of the input traces. This is the power of stack. In the paper, Liu et al. improve on the simple sum by weighting the traces adaptively. Click to enlarge.
Here's another example, but with real data. This is part of Figure 3 from Liu, G, S Fomel, L Jin, and X Chen (2009). Stacking seismic data using local correlation. Geophysics 74 (2) V43–V48. On the left is an NMO-corrected (flattened) common mid-point gather from a 2D synthetic model with Gaussian noise added. These 12 traces each came from a single receiver, though in this synthetic case the receiver was a virtual one. Now we can add the 12 traces to get a single trace, which has much stronger signal, relative to the background noise, than any of the input traces. This is the power of stack. In the paper, Liu et al. improve on the simple sum by weighting the traces adaptively. Click to enlarge.
The number of traces available for the stack is called fold. The examples above have folds of 20 and 12. Geophysicists like fold. Fold works. Let's look at another example.
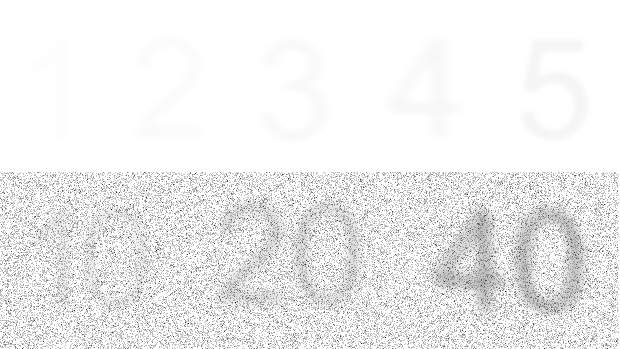
Above, I've made a single digit 1 with 1% opacity — it's almost invisible. If I stack two 2s, with a little random jitter, the situation is still desperate. When I have five digits, I can at least see the hidden image with some fidelity. However, if I add random noise to the image, a fold of 5 is no longer enough. I need at least 10, and ideally more like 20 images stacked up to see any signal. So it is for seismic data: to see through the noise, we need fold.
Now you know a bit about why we want more traces from the field, next time I'll look at how much those traces cost, and how to figure out how many you need.
Thank you to Stuart Mitchell of Calgary for the awesome analogy for seismic fold.








 Except where noted, this content is licensed
Except where noted, this content is licensed