The Surmont Supermerge

In my recent Abstract horror post, I mentioned an interesting paper in passing, Durkin et al. (2017):

Paul R. Durkin, Ron L. Boyd, Stephen M. Hubbard, Albert W. Shultz, Michael D. Blum (2017). Three-Dimensional Reconstruction of Meander-Belt Evolution, Cretaceous Mcmurray Formation, Alberta Foreland Basin, Canada. Journal of Sedimentary Research 87 (10), p 1075–1099. doi: 10.2110/jsr.2017.59

I wanted to write about it, or rather about its dataset, because I spent about 3 years of my life working on the USD 75 million seismic volume featured in the paper. Not just on interpreting it, but also on acquiring and processing the data.

Let's start by feasting our eyes on a horizon slice, plus interpretation, of the Surmont 'Supermerge' 3D seismic volume:

Figure 1 from Durkin et al (2017), showing a stratal slice from 10 ms below the top of the McMurray Formation (left), and its interpretation (right). © 2017, SEPM (Society for Sedimentary Geology) and licensed CC-BY.

A decade ago, I was 'geophysics advisor' on Surmont, which is jointly operated by ConocoPhillips Canada, where I worked, and Total E&P Canada. My line manager was a Total employee; his managers were ex-Gulf Canada. It was a fantastic, high-functioning team, and working on this project had a profound effect on me as a geoscientist. 

The Surmont bitumen field

The dataset covers most of the Surmont lease, in the giant Athabasca Oil Sands play of northern Alberta, Canada. The Surmont field alone contains something like 25 billions barrels of bitumen in place. It's ridiculously massive — you'd be delighted to find 300 million bbl offshore. Given that it's expensive and carbon-intensive to produce bitumen with today's methods — steam-assisted gravity drainage (SAGD, "sag-dee") in Surmont's case — it's understandable that there's a great deal of debate about producing the oil sands. One factoid: you have to burn about 1 Mscf or 30 m³ of natural gas, costing about USD 10–15, to make enough steam to produce 1 bbl of bitumen.

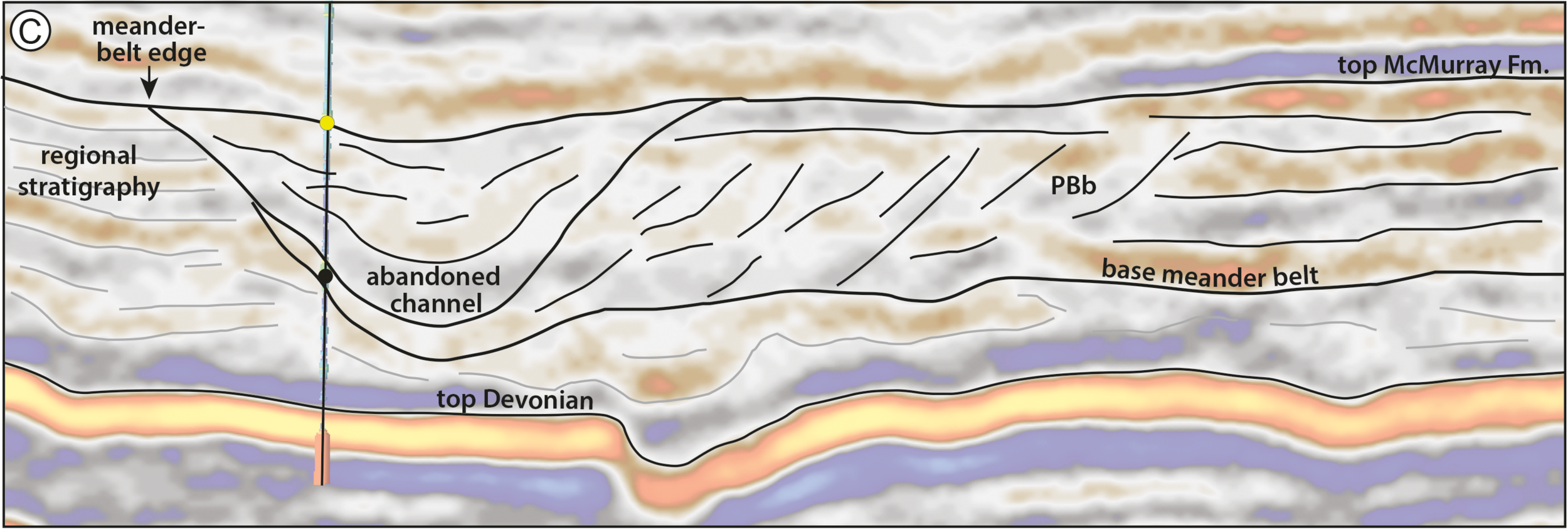
Detail from Figure 12 from Durkin et al (2017), showing a seismic section through the McMurray Formation. Most of the abandoned channels are filled with mudstone (really a siltstone). The dipping heterolithic strata of the point bars, so obvious in horizon slices, are quite subtle in section. © 2017, SEPM (Society for Sedimentary Geology) and licensed CC-BY.

The field is a geoscience wonderland. Apart from the 600 km² of beautiful 3D seismic, there are now about 1500 wells, most of which are on the 3D. In places there are more than 20 wells per section (1 sq mile, 2.6 km², 640 acres). Most of the wells have a full suite of logs, including FMI in 2/3 wells and shear sonic as well in many cases, and about 550 wells now have core through the entire reservoir interval — about 65–75 m across most of Surmont. Let that sink in for a minute.

What's so awesome about the seismic?

OK, I'm a bit biased, because I planned the acquisition of several pieces of this survey. There are some challenges to collecting great data at Surmont. The reservoir is only about 500 m below the surface. Much of the pay sand can barely be called 'rock' because it's unconsolidated sand, and the reservoir 'fluid' is a quasi-solid with a viscosity of 1 million cP. The surface has some decent topography, and the near surface is glacial till, with plenty of boulders and gravel-filled channels. There are surface lakes and the area is covered in dense forest. In short, it's a geophysical challenge.

Nonetheless, we did collect great data; here's how:

• General information
• The ca. 600 km² Supermerge consists of a dozen 3Ds recorded over about a decade starting in 2001.
• The northern 60% or so of the dataset was recombined from field records into a single 3D volume, with pre- and post-stack time imaging.
• The merge was performed by CGG Veritas, cost nearly $2 million, and took about 18 months.
• Geometry
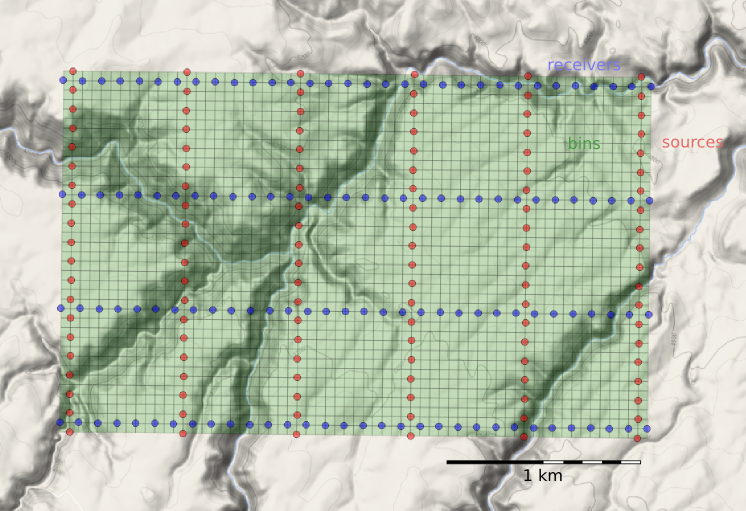
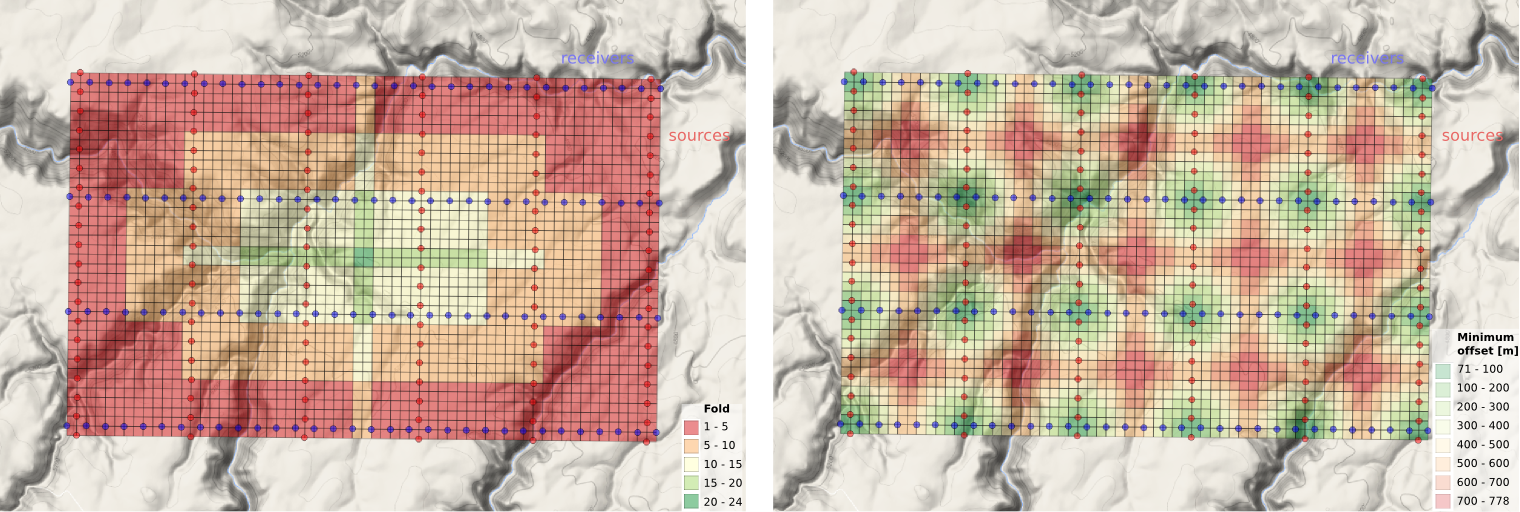
• Most of the surveys had a 20 m shot and receiver spacing, giving the volume a 10 m by 10 m natural bin size
• The original survey had parallel and coincident shot and receiver lines (Megabin); later surveys were orthogonal.
• We varied the line spacing between 80 m and 160 m to get trace density we needed in different areas.
• Sources
• Some surveys used 125 g dynamite at a depth of 6 m; others the IVI EnviroVibe sweeping 8–230 Hz.
• We used an airgun on some of the lakes, but the data was terrible so we stopped doing it.
• Receivers
• Most of the surveys were recorded into single-point 3C digital MEMS receivers planted on the surface.
• Bandwidth
• Most of the datasets have data from about 8–10 Hz to about 180–200 Hz (and have a 1 ms sample interval).

The planning of these surveys was quite a process. Because access in the muskeg is limited to 'freeze up' (late December until March), and often curtailed by wildlife concerns (moose and elk rutting), only about 6 weeks of shooting are possible each year. This means you have to plan ahead, then mobilize a fairly large crew with as many channels as possible. After acquisition, each volume spent about 6 months in processing — mostly at Veritas and then CGG Veritas, who did fantastic work on these datasets.

Kudos to ConocoPhillips and Total for letting people work on this dataset. And kudos to Paul Durkin for this fine piece of work, and for making it open access. I'm excited to see it in the open. I hope we see more papers based on Surmont, because it may be the world's finest subsurface dataset. I hope it is released some day, it would have huge impact.

---

References & bibliography

Paul R. Durkin, Ron L. Boyd, Stephen M. Hubbard, Albert W. Shultz, Michael D. Blum (2017). Three-Dimensional Reconstruction of Meander-Belt Evolution, Cretaceous Mcmurray Formation, Alberta Foreland Basin, Canada. Journal of Sedimentary Research 87 (10), p 1075–1099. doi: 10.2110/jsr.2017.59 (not live yet).

Hall, M (2007). Cost-effective, fit-for-purpose, lease-wide 3D seismic at Surmont. SEG Development and Production Forum, Edmonton, Canada, July 2007.

Hall, M (2009). Lithofacies prediction from seismic, one step at a time: An example from the McMurray Formation bitumen reservoir at Surmont. Canadian Society of Exploration Geophysicists National Convention, Calgary, Canada, May 2009. Oral paper.

Zhu, X, S Shaw, B Roy, M Hall, M Gurch, D Whitmore and P Anno (2008). Near-surface complexity masquerades as anisotropy. SEG Annual Convention, Las Vegas, USA, November 2008. Oral paper. doi: 10.1190/1.3063976.

Surmont SAGD Performance Review (2016), by ConocoPhillips and Total geoscientists and engineers. Submitted to AER, 258 pp. Available online [PDF] — and well worth looking at.

Trad, D, M Hall, and M Cotra (2008). Reshooting a survey by 5D interpolation. Canadian Society of Exploration Geophysicists National Convention, Calgary, Canada, May 2006. Oral paper. 

Seismic survey layout: from theory to practice

Up to this point, we've modeled the subsurface moveout and the range of useful offsets, we've build an array of sources and receivers, and we've examined the offset and azimuth statistics in the bins. And we've done it all using open source Python libraries and only about 100 lines of source code. What we have now is a theoretical seismic program. Now it's time to put that survey on the ground. 

The theoretical survey

Ours is a theoretical plot because it idealizes the locations of sources and receivers, as if there were no surface constraints. But it's unlikely that we'll be able to put sources and receivers in perfectly straight lines and at perfectly regular intervals. Topography, ground conditions, buildings, pipelines, and other surface factors have an impact on where stations can't be placed. One of the jobs of the survey designer is to indicate how far sources and receivers can be skidded, or moved away from their theoretical locations before rejecting them entirely.

From theory to practice

In order to see through the noise, we need to collect lots of traces with plenty of redundancy. The effect of station gaps or relocations won't be as immediately obvious as dead pixels on a digital camera, but they can cause some bins to have fewer traces than the idealized layout, which could be detrimental to the quality of imaging in that region. We can examine the impact of moving and removing stations on the data quality, by recomputing the bin statistics based on the new geometries, and comparing them to the results we were designing for. 

When one station needs to be adjusted, it may make sense to adjust several neighbouring points to compensate, or to add more somewhere nearby. But how can we tell what makes sense? The points should resemble the idealized fold and minimum offset statistics bin by bin. For example, let's assume that we can't put sources or receivers in river valleys and channels. Say they are too steep, or water would destroy the instrumentation, or are otherwise off limits. So we remove the invalid points from our series, giving our survey a more realistic surface layout based on the ground conditions. 

Unlike the theoretical layout, we now have bins that aren't served by any traces at all so we've made them invisible (no data). On the right, bins that have a minimum offset greater than 800 m are highlighted in grey. Beneath these grey bins is where the onset of imaging would be the deepest, which would not be a good thing if we have interests in the shallow part of the subsurface. (Because seismic energy spreads out more or less spherically from the source, we will eventually undershoot all but the largest gaps.)

This ends the mini-series on seismic acquisition. I'll end with the final state of the IPython Notebook we've been developing, complete with the suggested edits of reader Jake Wasserman in the last post — this single change resulted in a speed-up of the midpoint-gathering step from about 30 minutes to under 30 seconds!

We want to know... How do you plan seismic acquisitions? Do you have a favourite back-of-the-envelope calculation, a big giant spreadsheet, or a piece of software you like? Let us know in the comments.

It goes in the bin

The cells of a digital image sensor. CC-BY-SA Natural Philo.

Inlines and crosslines of a 3D seismic volume are like the rows and columns of the cells in your digital camera's image sensor. Seismic bins are directly analogous to pixels — tile-like containers for digital information. The smaller the tiles, the higher the maximum realisable spatial resolution. A square survey with 4 million bins (or 4 megapixels) gives us 2000 inlines and 2000 crosslines to interpret, after processing the data of course. Small bins can mean high resolution, but just as with cameras, bin size is only one aspect of image quality.

Unlike your digital camera however, seismic surveys don't come with a preset number of megapixels. There aren't any bins until you form them. They are an abstraction.

Making bins

This post picks up where Laying out a seismic survey left off. Follow the link to refresh your memory; I'll wait here. 

At the end of that post, we had a network of sources and receivers, and the Notebook showed how I computed the midpoints of the source–receiver pairs. At the end, we had a plot of the midpoints. Next we'd like to collect those midpoints into bins. We'll use the so-called natural bins of this orthogonal survey — squares with sides half the source and receiver spacing.

Just as we represented the midpoints as a GeoSeries of Point objects, we will represent  the bins with a GeoSeries of Polygons. GeoPandas provides the GeoSeries; Shapely provides the geometries; take a look at the IPython Notebook for the code. This green mesh is the result, and will hold the stacked traces after processing.

Fetching the traces within each bin

To create a CMP gather like the one we modelled at the start, we need to grab all the traces that have midpoints within a particular bin. And we'll want to create gathers for every bin, so it is a huge number of comparisons to make, even for a small example such as this: 128 receivers and 120 sources make 15 320 midpoints. In a purely GIS environment, we could perform a spatial join operation between the midpoint and bin GeoDataFrames, but instead we can use Shapely's contains method inside nested loops. Because of the loops, this code block takes a long time to run.

# Make a copy because I'm going to drop points as I
# assign them to polys, to speed up subsequent search.
midpts = midpoints.copy()

offsets, azimuths = [], [] # To hold complete list.

# Loop over bin polygons with index i.
for i, bin_i in bins.iterrows():
    
    o, a = [], [] # To hold list for this bin only.
    
    # Now loop over all midpoints with index j.
    for j, midpt_j in midpts.iterrows():
        if bin_i.geometry.contains(midpt_j.geometry):
            # Then it's a hit! Add it to the lists,
            # and drop it so we have less hunting.
            o.append(midpt_j.offset)
            a.append(midpt_j.azimuth)
            midpts = midpts.drop([j])
            
    # Add the bin_i lists to the master list
    # and go around the outer loop again.
    offsets.append(o)
    azimuths.append(a)
    
# Add everything to the dataframe.    
bins['offsets'] = gpd.GeoSeries(offsets)
bins['azimuths'] = gpd.GeoSeries(azimuths)

After we've assigned traces to their respective bins, we can make displays of the bin statistics. Three common views we can look at are:

1. A spider plot to illustrate the offset and azimuth distribution.
2. A heat map of the number of traces contributing to each bin, usually called fold.
3. A heat map of the minimum offset that is servicing each bin. 

The spider plot is easily achieved with Matplotlib's quiver plot:

And the arrays representing our data are also quite easy to display as heatmaps of fold (left) and minimum offset (right): 

In the next and final post of this seismic survey mini-series, we'll analyze the impact of data quality when there are gaps and shifts in the source and receiver stations from these idealized locations.

Last thought: if the bins of a seismic survey are like a digital camera's image sensor, then what is the apparatus that acts like a lens? 

Laying out a seismic survey

Cutlines for a dense 3D survey at Surmont field, Alberta, Canada. Image: Google Maps.

Cutlines for a dense 3D survey at Surmont field, Alberta, Canada. Image: Google Maps.There are a number of ways to lay out sources and receivers for a 3D seismic survey. In forested areas, a designer may choose a pattern that minimizes the number of trees that need to be felled. Where land access is easier, designers may opt for a pattern that is efficient for the recording crew to deploy and pick up receivers. However, no matter what survey pattern used, most geometries consist of receivers strung together along receiver lines and source points placed along source lines. The pairing of source points with live receiver stations comprises the collection of traces that go into making a seismic volume.

An orthogonal surface pattern, with receiver lines laid out perpendicular to the source lines, is the simplest surface geometry to think about. This pattern can be specified over an area of interest by merely choosing the spacing interval between lines well as the station intervals along the lines. For instance:

xmi = 575000        # Easting of bottom-left corner of grid (m)
ymi = 4710000       # Northing of bottom-left corner (m)
SL = 600            # Source line interval (m)
RL = 600            # Receiver line interval (m)
si = 100            # Source point interval (m)
ri = 100            # Receiver point interval (m)
x = 3000            # x extent of survey (m)
y = 1800            # y extent of survey (m)

We can calculate the number of receiver lines and source lines, as well as the number of receivers and sources for each.

# Calculate the number of receiver and source lines.
rlines = int(y/RL) + 1
slines = int(x/SL) + 1

# Calculate the number of points per line (add 2 to straddle the edges). 
rperline = int(x/ri) + 2 
sperline = int(y/si) + 2

# Offset the receiver points.
shiftx = -si/2.
shifty = -ri/2.

Computing coordinates

We create a list of x and y coordinates with a nested list comprehension — essentially a compact way to write 'for' loops in Python — that iterates over all the stations along the line, and all the lines in the survey.

# Find x and y coordinates of receivers and sources.
rcvrx = [xmi+rcvr*ri+shifty for line in range(rlines) for rcvr in range(rperline)]
rcvry = [ymi+line*RL+shiftx for line in range(rlines) for rcvr in range(rperline)]

srcx = [xmi+line*SL for line in range(slines) for src in range(sperline)]
srcy = [ymi+src*si for line in range(slines) for src in range(sperline)]

To make a map of the ideal surface locations, we simply pass this list of x and y coordinates to a scatter plot:

Plotting these lists is useful, but it is rather limited by itself. We're probably going to want to do more calculations with these points — midpoints, azimuth distributions, and so on — and put these data on a real map. What we need is to insert these coordinates into a more flexible data structure that can hold additional information.

Shapely, Pandas, and GeoPandas

Shapely is a library for creating and manipulating geometric objects like points, lines, and polygons. For example, Shapely can easily calculate the (x, y) coordinates halfway along a straight line between two points.

Pandas provides high-performance, easy-to-use data structures and data analysis tools, designed to make working with tabular data easy. The two primary data structures of Pandas are:

• Series — a one-dimensional labelled array capable of holding any data type (strings, integers, floating point numbers, lists, objects, etc.)
• DataFrame — a 2-dimensional labelled data structure where the columns can contain many different types of data. This is similar to the NumPy structured array but much easier to use.

GeoPandas combines the capabilities of Shapely and Pandas and greatly simplifies geospatial operations in Python, without the need for a spatial database. GeoDataFrames are a special case of DataFrames that are specifically for representing geospatial data via a geometry column. One awesome thing about GeoDataFrame objects is they have methods for saving data to shapefiles.

So let's make a set of (x,y) pairs for receivers and sources, then make Point objects using Shapely, and in turn add those to GeoDataFrame objects, which we can write out as shapefiles:

# Zip into x,y pairs.
rcvrxy = zip(rcvrx, rcvry)
srcxy = zip(srcx, srcy)

# Create lists of shapely Point objects.
rcvrs = [Point(x,y) for x,y in rcvrxy]
srcs = [Point(x,y) for x,y in srcxy]

# Add lists to GeoPandas GeoDataFrame objects.
receivers = GeoDataFrame({'geometry': rcvrs})
sources = GeoDataFrame({'geometry': srcs})

# Save the GeoDataFrames as shapefiles.
receivers.to_file('receivers.shp')
sources.to_file('sources.shp')

It's a cinch to fire up QGIS and load these files as layers on top of a satellite image or physical topography map. As a survey designer, we can now add, delete, and move source and receiver points based on topography and land issues, sending the data back to Python for further analysis.

All the code used in this post is in an IPython notebook. You can read it, and even execute it yourself. Put your own data in there and see how it comes out!

NEWSFLASH — If you think the geoscientists in your company would like to learn how to play with geological and geophysical models and data — exploring seismic acquisition, or novel well log displays — we can come and get you started! Best of all, we'll help you get up and running on your own data and your own ideas.

If you or your company needs a dose of creative geocomputing, check out our new geocomputing course brochure, and give us a shout if you have any questions. We're now booking for 2015.

The race for useful offsets

We've been working on a 3D acquisition lately. One of the factors influencing the layout pattern of sources and receivers in a seismic survey is the range of useful offsets over the depth interval of interest. If you've got more than target depth, you'll have more than one range of useful offsets. For shallow targets this range is limited to small offsets, due to direct waves and first breaks. For deeper targets, the range is limited at far offsets by energy losses due to geometric spreading, moveout stretch, and system noise.

In seismic surveying, one must choose a spacing interval between geophones along a receiver line. If phones are spaced close together, we can collect plenty of samples in a small area. If the spacing is far apart, the sample density goes down, but we can collect data over a bigger area. So there is a trade-off and we want to maximize both; high sample density covering the largest possible area.

What are useful offsets?

It isn't immediately intuitive why illuminating shallow targets can be troublesome, but with land seismic surveying in particular, first breaks and near surface refractions clobber shallow reflecting events. In the CMP domain, these are linear signals, used for determining statics, and are discarded by muting them out before migration. Reflections that arrive later than the direct wave and first refractions don't get muted out. But if these reflections arrive later than the air blast noise or ground roll noise — pervasive at near offsets — they get caught up in noise too. This region of the gather isn't muted like the top mute, otherwise you'd remove the data at near offsets. Instead, the gathers are attacked with algorithms to eliminate the noise. The extent of each hyperbola that passes through to migration is what we call the range of useful offsets.

The deepest reflections have plenty of useful offsets. However if we wanted to do adequate imaging somewhere between the first two reflections, for instance, then we need to make sure that we record redundant ray paths over this smaller range as well. We sometimes call this aperture; the shallow reflection is restricted in the number of offsets that it can be illuminated with, the deeper reflections can tolerate an aperture that is more open. In this image, I'm modelling the case of 60 geophones spanning 3000 metres, spaced evenly at 100 metres apart. This layout suggests merely 4 or 5 ray paths will hit the uppermost reflection, the shortest ray paths at small offsets. Also, there is usually no geophone directly on top of the source location to record a vertical ray path at zero offset. The deepest reflections however, should have plenty of fold, as long as NMO stretch, geometric spreading, and noise levels were good.

The problem with determining the range of useful offsets by way of a model is, not only does it require a velocity profile, which is easily attained from a sonic log, VSP, or velocity analysis, but it also requires an estimation of the the speed, intensity, and duration of the near surface events to be muted. Parameters that depend largely on the nature of the source and the local ground conditions, which vary from place to place, and from one season to the next.

In a future post, we'll apply this notion of useful offsets to build a pattern for shooting a 3D.

---

Click here for details on how I created this figure using the IPython Notebook. If you don't have it, IPython is easy to install. The easiest way is to install all of scientific Python, or use Canopy or Anaconda.

This post was inspired in part by Norm Cooper's 2004 article, A world of reality: Designing 3D seismic programs for signal, noise, and prestack time-migration. The Leading Edge23 (10), 1007-1014.DOI: 10.1190/1.1813357

Update on 2014-12-17 13:04 by Matt Hall
Don't miss the next installment — Laying out a seismic survey — with more IPython goodness!

Great geophysicists #9: Ernst Chladni

Ernst Chladni was born in Wittenberg, eastern Germany, on 30 November 1756, and died 3 April 1827, at the age of 70, in the Prussian city of Breslau (now Wrocław, Poland). Several of his ancestors were learned theologians, but his father was a lawyer and his mother and stepmother from lawyerly families. So young Ernst did well to break away into a sound profession, ho ho, making substantial advances in acoustic physics. 

Chladni, 'the father of acoustics', conducted a large number of experiments with sound, measuring the speed of sound in various solids, and — more adventurously — in several gases too, including oxygen, nitrogen, and carbon dioxode. Interestingly, though I can find only one reference to it, he found that the speed of sound in Pinus sylvestris was 25% faster along the grain, compared to across it — is this the first observation of acoustic anisotropy? 

The experiments Chladni is known for, however, are the plates. He effectively extended the 1D explorations of Euler and Bernoulli in rods, and d'Alembert in strings, to the 2D realm. You won't find a better introduction to Chladni patterns than this wonderful blog post by Greg Gbur. Do read it — he segués nicely into quantum mechanics and optics, firmly linking Chladni with the modern era. To see the patterns forming for yourself, here's a terrific demonstration (very loud!)...

The drawings from Chladni's book Die Akustik are almost as mesmerizing as the video. Indeed, Chladni toured most of mainland Europe, demonstrating the figures live to curious Enlightenment audiences. When I look at them, I can't help wondering if there is some application for exploration geophysics — perhaps we are missing something important in the wavefield when we sample with regular acquisition grids?

References

Chladni, E, Die Akustik, Breitkopf und Härtel, Leipzig, 1830. Amazingly, this publishing company still exists.

Read more about Chladni in Wikipedia and in monoskop.org — an amazing repository of information on the arts and sciences. 

This post is part of a not-very-regular series of posts on important contributors to geophysics. It's going rather slowly — we're still in the eighteenth century. See all of them, and do make suggestions if we're missing some!

A revolution in seismic acquisition?

We're in warm, sunny Calgary for the GeoConvention 2013. The conference feels like it's really embracing geophysics this year — in the past it's always felt more geological somehow. Even the exhibition floor felt dominated by geophysics. Someone we spoke to speculated that companies were holding their geological cards close to their chests, but the service companies are still happy to talk about (ahem, promote) their geophysical advances.

Are you at the conference? What do you think? Let us know in the comments.

We caught about 15 talks of the 100 or so on offer today. A few of them ignited the old whines about half-cocked proofs of efficacy. Why is it still acceptable to say that a particular seismic volume or inversion result is 'higher resolution' or 'more geological' with nothing more than a couple of sections or timeslices as evidence?

People are excited about designing seismic acquisition expressly for wavefield reconstruction. In a whole session devoted to the subject, for example, Mauricio Sacchi showed how randomization helps with regularization in processing, allowing us to either get better image quality, or to lower cost. It feels like the start of a new wave of innovation in acquisition, which has more than its fair share of recent innovation: multi-component, wide azimuth, dual-sensor, simultaneous source...

Is it a revolution? Or just the fallacy of new things looking revolutionary... until the next new thing? It's intriguing to the non-specialist. People are talking about 'beyond Nyquist' again, but this time without inducing howls of derision. We just spent an hour talking about it, and we think there's something deep going on... we're just not sure how to articulate it yet.

Unsolved problems

We were at the conference today, but really we are focused on the session we're hosting tomorrow morning. Along with a roomful of adventurous conference-goers (you're invited too!), looking for the most pressing questions in subsurface science. We start at 8 a.m. in Telus 101/102 on the main floor of the north building.

O is for Offset

Offset is one of those jargon words that geophysicists kick around without a second thought, but which might bewilder more geological interpreters. Like most jargon words, offset can mean a couple of different things: 

• Offset distance, which is usually what is meant by simply 'offset'.
• Offset angle, which is often what we really care about.
• We are not talking about offset wells, or fault offset.

What is offset?

Sherriff's Encyclopedic Dictionary is characteristically terse:

Offset: The distance from the source point to a geophone or to the center of a geophone group.

The concept of offset only really makes sense in the pre-stack world — to field data and gathers. The traces in stacked data (everyday seismic volumes) combine data from many offsets. So let's look at the geometry of seismic acquisition. A map shows the layout of shots (red) and receivers (blue). We can define offset and azimuth A at the midpoint of every shot–receiver pair, on a map (centre) and in section (right):

Offset distance applies to traces. The offset distance is the straight-line distance from the vibrator, shot-hole or air-gun (or any other source) to the particular receiver that recorded the trace in question. If we know the geometry of the acquisition, and the size of the recording patch or length of the streamers, then we can calculate offset distance exactly. 

Offset angle applies to specific samples on a trace. The offset angle is the incident angle of the reflected ray that that a given sample represents. Samples at the top of a trace have larger offset angles than those at the bottom, even though they have the same offset distance. To compute these angles, we need to know the vertical distances, and this requires knowledge of the velocity field, which is mostly unknown. So offset angle is not objective, but a partly interpreted quantity.

Why do we care?

Acquiring longer offsets can help undershoot gaps in a survey, or image beneath salt canopies and other recumbent features. Longer offsets also helps with velocity estimation, because we see more moveout.

Looking at how the amplitude of a reflection changes with offset is the basis of AVO analysis. AVO analysis, in turn, is the basis of many fluid and lithology prediction techniques.

Offset is one of the five canonical dimensions of pre-stack seismic data, along with inline, crossline, azimuth, and frequency. As such, it is a key part of the search for sparsity in the 5D interpolation method perfected by Daniel Trad at CGGVeritas. 

Recently, geophysicists have become interested not just in the angle of a reflection, but in the orientation of a reflection too. This is because, in some geological circumstances, the amplitude of a reflection depends on the orientation with respect to the compass, as well as the incidence angle. For example, looking at data in both of these dimensions can help us understand the earth's stress field.

Offset is the characteristic attribute of pre-stack seismic data. Seismic data would be nothing without it.

Brittleness and robovibes

Day 3 of the SEG Annual Meeting was just as rammed with geophysics as the previous two days. I missed this morning's technical program, however, as I've taken on the chairpersonship (if that's a word) of the SEG Online Committee. So I had fun today getting to grips with that business. Aside: if you have opinion's about SEG's online presence, please feel free to send them my way.

Here are my highlights from the rest of the day — both were footnotes in their respective talks:

Brittleness — Lev Vernick, Marathon

Evan and I have had a What is brittleness? post in our Drafts folder for almost two years. We're skeptical of the prevailing view that a shale's brittleness is (a) a tangible rock property and (b) a function of Young's modulus and Poisson's ratio, as proposed by Rickman et al. 2008, SPE 115258. To hear such an intellect as Lev declare the same today convinced me that we need to finish that post — stay tuned for that. Bottom line: computing shale brittleness from elastic properties is not physically meaningful. We need to find more appropriate measures of frackability, [Edit, May 2015; Vernik tells me the following bit is the opposite of what he said, apologies for my cloth ears...] which Lev pointed out is, generally speaking, inversely proportional to organic content. This poses a basic conflict for those exploiting shale plays. [End of public service announcement.]

Robovibes — Guus Berkhout, TU Delft

At least 75% of Berkhout's talk went by me today, mostly over my head. I stopped writing notes, which I only do when I'm defeated. But once he'd got his blended source stuff out of the way, he went rogue and asked the following questions:

1. Why do we combine all seismic frequencies into the device? Audio got over this years ago (right).
2. Why do we put all the frequencies at the same location? Viz 7.1 surround sound.
3. Why don't we try more crazy things in acquisition?

I've wondered the same thing myself — thinking more about the receiver side than the sources — after hearing about the brilliant sampling strategy the Square Kilometer Array is using at a PIMS Lunchbox Lecture once. But Berkhout didn't stop at just spreading a few low-frequency vibrators around the place. No, he wants robots. He wants an autonomous army of flying and/or floating narrow-band sources, each on its own grid, each with its own ghost matching, each with its own deblending code. This might be the cheapest million-channel acquisition system possible. Berkhout's aeronautical vibrator project starts in January. Seriously.

More posts from SEG 2012.

Speaker image is licensed CC-BY-SA by Tobias Rütten, Wikipedia user Metoc.

Fold for sale

A few weeks ago I wrote a bit about seismic fold, and why it's important for seeing through noise. But how do you figure out the fold of a seismic survey?

The first thing you need to read is Norm Cooper's terrific two-part land seismic tutorial. One of his main points is that it's not really fold we should worry about, it's trace density. Essentially, this normalizes the fold by the area of the natural bins (the areal patches into which we will gather traces for the stack). Computing trace density, given effective maximum offset X_max (or depth, in a pinch), source and receiver line spacings S and R, and source and receiver station intervals s and r:

Cooper helpfully gave ballpark ranges for increasingly hard imaging problems. I've augmented it, based on my own experience. Your mileage may vary! (Edit this table)

Traces cost money

So we want more traces. The trouble is, traces cost money. The chart below reflects my experiences in the bitumen sands of northern Alberta (as related in Hall 2007). The model I'm using is a square land 3D with an orthogonal geometry and no overlaps (that is, a single swath), and 2007 prices. A trace density of 50 traces/km² is equivalent to a fold of 5 at 500 m depth. As you see, the cost of seismic increases as we buy more traces for the stack. Fun fact: at a density of about 160 000 traces/km², the cost is exactly $1 per trace. The good news is that it increases with the square root (more or less), so the incremental cost of adding more traces gets progressively cheaper:

Given that you have limited resources, your best strategy for hitting the 'sweet spot'—if there is one—is lots and lots of testing. Keep careful track of what things cost, so you can compute the probable cost benefit of, say, halving the trace density. With good processing, you'll be amazed what you can get away with, but of course you risk coping badly with unexpected problems in the near surface.

What do you think? How do you make decisions about seismic geometry and trace density?

References

Cooper, N (2004). A world of reality—Designing land 3D programs for signal, noise, and prestack migration, Parts 1 and 2. The Leading Edge. October and December, 2004. 

Hall, M (2007). Cost-effective, fit-for-purpose, lease-wide 3D seismic at Surmont. SEG Development and Production Forum, Edmonton, Canada, July 2007.