What is a darcy?

/

Permeability is the capacity of a porous material to transmit fluids. The SI unit of permeability is m2 (area) but the units adopted by the petroleum industry have been named after Henry Darcy, who derived Darcy's law. A darcy is a confusing jumble of units which combines a standardized set of laboratory experiments. By definition, a material of 1 darcy permits a flow of 1 cm3/s of a fluid with viscosity 1 cP (1 mPa.s) under a pressure gradient of 1 atm/cm across an area of 1 cm2.

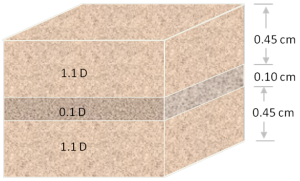
Apart from having obscure units with an empirical origin, permeability can be an incredibly variable quantity. It can vary be as low as 10–9 D for tight gas reservoirs and shale, to 101 D for unconsolidated conventional reservoirs. Just as electrical resistivity, values are plotted on a logarithmic scale. Many factors such as rock type, pore size, shape and connectedness and can effect fluid transport over volume scales from millimetres to kilometres.

Okay then, with that said, what is the upscaled permeability of the cube of rock shown here? In other words, if you only had to find one number to describe the permeability of this sample, what would it be? I'll pause for a moment while you grab your calculator... Okay, got an answer? What is it?

Read More

Aerial geology

/

A few recent posts by others on aerial geology prompted me to gather them for future reference. Please add any I've missed to the comments!

Large collections

Both of these pages features lots of pictures from all over the United States, plus a few from other parts of the world. I was a bit surprised not to find collections of geological pictures taken from helicopters or hot air balloons. 

  •  John Louie's Aerial Geology with lots of images taken from commercial aircraft (like the one shown at right, of the Clayton Valley dunes in Nevada; from John's site).
  • Geology by Lightplane by flying geologist Louis Maher and photographer Charles Mansfield has dozens of pictures taken from a Cessna mostly during the late 1950's and early 1960's. Doc Searl's blog post (below) is about this wonderful collection.

Blog posts

Publications

Great geophysicists #1: Ibn Sahl

/

Abu Sa’d al-’Ala’ ibn Sahl was a mathematician in late 10th Century Persia, working for the hugely powerful Abbasid caliphate and probably based in Baghdad. He understood the mathematics of refraction, at least six hundred years before Dutchman Willebrord Snellius wrote it all down and eventually gave the sine law of refraction his name. Snellius’ ancestors in Europe, in Ibn Sahl’s time, were in the middle of the Dark Ages, waiting patiently for the Renaissance just three or four hundred years away. I'll tell more about Snellius in a future post.

Refraction—the bending of a wave's ray-path due to a change in velocity—had been studied by the Egyptian astronomer Ptolemy in the second century, but he was unable to figure out the mathematics fully. It’s not known whether Ibn Sahl knew of this work, but Ptolemy’s Optics was certainly translated into Arabic, so it seems likely that he did. There wasn’t, after all, that much to read in those days.

The key figure from his work On Burning Mirrors and Lenses is shown here. I have cropped out part of the figure; see the whole thing on Wikipedia. I redrew the diagram, and added some annotation to show how it relates to the usual formulation of Snell's Law. The ratio of the lengths of the hypotenuses AB to DB is equal to the reciprocal of the ratio of the refractive indices of the materials on either side of the vertical line. Phew!

Ibn Sahl’s work was brought much further along by one of his successors, Ibn Haitham, widely considered to be the founding father of optics. He was the first person to make a pinhole camera, and thereby prove that light travelled in straight lines.

In Our Time

/

When I lived in Calgary I walked 25 minutes to and from work every day. Melvyn Bragg's weekly BBC radio programme was always one of my favourite things to listen to on the way. Every show has the same format: an informal forty-minute discussion with three academics. But the quintessence of In Our Time is its diversity of topics: Avicenna to Yeats to the Aeneid to Zoroastrianism.

Over the years, Bragg and his guests have covered lots of geological subjects. The wonderful BBC keeps the archive completely open, so you can listen to any show any time. Here are the most geoscientiferous ones I can find in the archive:

 

Here are some others, less directly related to geoscience:

 

Tomorrow's programme is on random and pseudo-randomness. Can't wait!

Rock physics and steam

/

Over the last few weeks, I have been revisiting and reminiscing over some past work, and found this poster I made for the 2007 SEG Development & Production Forum on the geophysics of heavy oil. A few months ago, the organizers of the workshop made a book out of many great articles that followed. Posters, however, often get printed only once, but that doesn't mean they need only be viewed once.

The poster illustrates the majority of my MSc thesis on the rock physics of steam injection in Canadian oil sands. You might be interested in this if you are interested in small scale seismic monitoring experiments, volume visualization, and novel seismic attributes for SAGD projects. For all you geocomputing enthusiasts, you'll recognize that all the figures were made with MathWorks MATLAB (something I hope to blog about later). It was a fun project, because it merged disparate data types, rock physics, finite-difference modeling, time-lapse seismic, and production engineering. There are a ton of subsurface problems that still need to be solved in oil sands, many opportunities to work across disciplines, and challenge the limits of our geoscience creativity. 

Here's the full reference: Bianco, E & D Schmitt (2007). High resolution modeling and monitoring of the SAGD process at the Athabasca tar sands: Underground Test Facility (UTF), 2007 SEG D&P Forum, Edmonton, Canada. If you prefer, you can grab these slides which I gave as an oral presentation on the same material, or flip to chapter 6 in the book.

Ripples

/

Yesterday I visited Sand Dollar Beach, near Lunenburg, with the kids. There's lots of room to run around: the beach has a 400 m wide foreshore, which means lots of shallow water at high tide (as in the Google Maps picture here). The low angle (less than half a degree) also sees the tide go in and out very quickly, allowing little time for reworking the delicate ripples. Their preservation is further helped by the fact that the waves along this sheltered coast are typically low-amplitude.


View Larger Map

At the edge of the just-visible stream cutting through the beach, the regular wave ripples, produced by oscillating currents, morph into more chaotic linguiod current ripples (right-hand side, mostly obscured by the stream). I can't say for sure, but the pattern may have been modified by animal tracks (deer, dog, dude?) during some previous low tide.

As I posted before, I am interested in the persistence of patterns across scales and even processes. For instance, this view (right) reminded me of blogger Silver Fox's recent post about the Basin and Range caterpillar army. An entirely different process: parallel morpholution.

If you look closely at the Google Map, above, you can see dim duneforms in the shallows, as a series of sub-parallel dark stripes. They echo the ripples in orientation and process, but have a wavelength of about 30 m. If you can't see them maybe this annotated version will help.

I would not claim to be an expert in the feeding traces of invertebrates, but I love taking pictures of them. I think the animals grazing in the cusps of these ripples were Chiridotea coeca, a tiny crustacean. You can read (a lot) more about them in Hauck et al (2008), Palaios 23, 336–343. According to these authors, such trails may be modern analogs of a rather common trace fossil called Nereites. 

Unsolved problems

/

One of the recurring dreams I've had this year is about unsolved problems. I've always loved these lists, the best known of which is perhaps the German David Hilbert's 1900 list of 23 unsolved problems in mathematics. There are several published versions of the list; take look at a later manuscript describing some of the problems.

A year or two ago, I read this meta-list in Wikipedia. Natch, I immediately wanted to create a list of unsolved problems in geoscience. It could help researches find big, interesting problems. It could help software developers focus their talents. It might just be a bit of fun. However, articles in Wikipedia need something to reference[citation needed], so even if I were capable of such a thing, one can't just sit down and hack one out. 

But you can try. Earlier this year, I drafted a proto-list for geophysics, drawn mostly from chats with friends. Please feel free to vote on the list, or add problems of your own. It is, I admit, a bit biased towards problems in seismology in pursuit of hydrocarbons. The list should be much broader, but I'm not yet the polymath I strive to be and quickly get out of my depth!

Here are the top five (per today) from my Google Moderator list of unsolved problems in geophysics:

  • How can we represent and quantify error and uncertainty from acquisition, through processing and interpretation, to analysis?
  • What useful signal or information can we extract from what we usually call 'noise' (multiples, refractions, reverberations, etc)?
  • How can we exploit the full spectrum in acquisition, processing, interpretation, and analysis?
  • Is there a 'best practice' for tying wells; if so, what is it?
  • What exactly is AVO-friendly processing?

What might a list of unsolved problems in geology look like? My likely-ignorant outlook suggests some:

  • Is it possible to predict the location, severity, and/or timing of earthquakes?
  • Do mantle plumes exist?
  • How do magnetic reversals happen?
  • Are mass extinctions cyclic?
  • Do the earth's physico-chemical systems mostly drive, or mostly respond to, changes in climate?
  • Does eustatic (global, synchronous, uniform) sea-level change happen, or does the ubiquity of local tectonism obviate the concept?
  • What exactly was the sequence of events that resulted in the end-Permian extinction? The end-Cretaceous?

I am proposing a workshop on the topic of unsolved problems in exploration and development geophysics at SEG next year in San Antonio. Ideas welcome.

Scale

/

One of the most persistent themes in geoscience is scale. Some properties of the earth are scale independent, or fractal; the shapes of rivers and coastlines, sediment grain shapes, and fracture size distributions might fall into this category. Other properties are scale dependent, such as statistical variance, seismic velocities (which are wavelength dependent), or stratigraphic stacking patterns.

Scale independent phenomena are common in nature, and in some human inventions. For example, Randall Munroe's brilliant comic today illustrating the solutions to tic-tac-toe (or noughts-and-crosses, as I'd call it). It's the optimal subset of the complete solution space, which shows its fractal nature completely.

The network of co-authorship relationships in SEG's journal Geophysics is also scale-free (most connected authors shown in red). From my 2010 paper in The Leading Edge.