What is anisotropy?
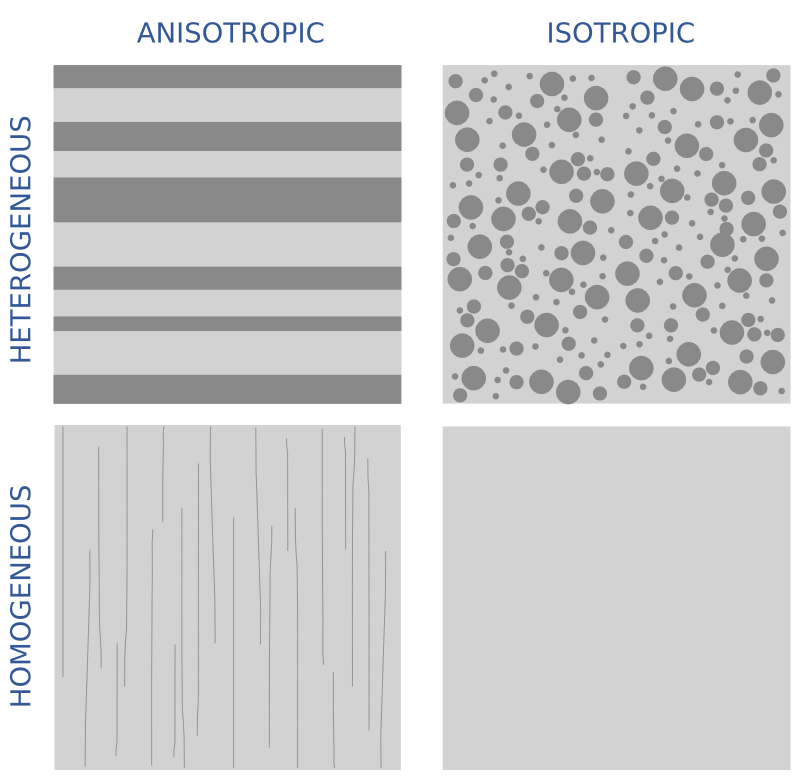
/Geophysicists often assume that the earth is isotropic. This word comes from 'iso', meaning same, and 'tropikos', meaning something to do with turning. The idea is that isotropic materials look the same in all directions — they have no orientation, and we can make measurements in any direction and get the same result. Note that this is different from homogeneous, which is the quality of uniformity of composition. You can think of anisotropy as a directional (not just spatial) variation in homogeneity.
In the illustration, I may have cheated a bit. The lower-left image shows a material that is homogeneous but anisotropic. The thin lines are supposed to indicate microfractures, say, or the alignment of clay flakes, or even just stress. So although the material has uniform composition, at least at this scale, it has an orientation.
The recognition of the earth's anisotropy is a dominant theme among papers in our forthcoming 52 Things book on rock physics. It's not exactly a new thing — it was an emerging trend 10 years ago when Larry Lines at U of C reviewed Milo Backus's famous 'challenges' (Lines 2005). And even then, the spread of anisotropic processing and analysis had been underway for almost 20 years since Leon Thomsen's classic 1986 paper, Weak elastic anisotropy. This paper introduced three parameters that we need—alongside the usual \(V_\text{P}\), \(V_\text{S}\), and \(\rho\)—to describe anisotropy. They are \(\delta\) (delta), \(\epsilon\) (epsilon), and \(\gamma\) (gamma), collectively referred to as Thomsen's parameters.
- \(\delta\) or delta — the short offset effect — captures the relationship between the velocity required to flatten gathers (the NMO velocity) and the zero-offset average velocity as recorded by checkshots. It's easy to measure, but perhaps hard to understand in physical terms.
- \(\epsilon\) or epsilon — the long offset effect — is, according to Thomsen himself: "the fractional difference between vertical and horizontal P velocities; i.e., it is the parameter usually referred to as 'the' anisotropy of a rock". Unfortunately, the horizontal velocity is rather hard to measure.
- \(\gamma\) or gamma — the shear wave effect — relates, as rock physics meister Colin Sayers put it on Twitter, a horizontal shear wave with horizontal polarization to a vertical shear wave. He added, "\(\gamma\) can be determined in a single well using sonic. So the correlation with \(\epsilon\) and \(\delta\) is of great interest."
Sidenote to aspiring authors: Thomsen's seminal paper, which has been cited over 2800 times, is barely 13 pages long. Three and a half of those pages are taken up by... data! A huge table containing the elastic parameters of almost 60 samples. And this is from a corporate scientist at Amoco. So no more excuses: publish you data! </rant>
Vertical transverse what now?
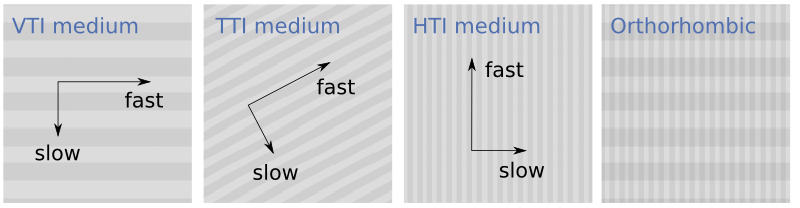
The other bit of jargon you will come across is the concept of transverse isotropy, which is a slightly perverse (to me) way of expressing the orientation of the anisotropy effect. In vertical transverse isotropy, the horizontal velocity is different from the vertical velocity. Think of flat-lying shales with gravity dominating the stress field. Usually, the velocity is faster along the beds than it is across the beds. This manifests as nonhyperbolic moveout in the far offsets, in particular a pull-up or 'hockey stick' effect in the gathers — the arrivals are unexpectedly early at long offsets. Clearly, this will also affect AVO analysis.
There's more jargon. If the rocks are dipping, we call it tilted transverse isotropy, or TTI. But if the anisotropies, so to speak, are oriented vertically — as with fractures, for example, or simply horizontal stress — then it's horizontal transverse isotropy, or HTI. This causes azimuthal (compass directional) travel-time variations. We can even venture into situations where we encounter orthorhombic anisotropy, as in the combined VTI/HTI model shown above. It's easy to imagine how these effects, if not accounted for in processing, can (and do!) result in suboptimal seismic images. Accounting for them is not easy though, and trying can do more harm than good.
If you have handy rules of thumb of ways of conceptualizing anisotropy, I'd love to hear about them. Some time soon I want to write about thin-layer anisotropy, which is where this post was going until I got sidetracked...
References
Lines, L (2005). Addressing Milo's challenges with 25 years of seismic advances. The Leading Edge 24 (1), 32–35. DOI 10.1190/1.2112389.
Thomsen, L (1986). Weak elastic anisotropy. Geophysics 51 (10), 1954–1966. DOI 10.1190/1.1442051.














 Except where noted, this content is licensed
Except where noted, this content is licensed