To make up microseismic
/I am not a proponent of making up fictitious data, but for the purposes of demonstrating technology, why not? This post is the third in a three-part follow-up from the private beta I did in Calgary a few weeks ago. You can check out the IPython Notebook version too. If you want more of this in person, sign up at the bottom or drop us a line. We want these examples to be easily readable, especially if you aren't a coder, so please let us know how we are doing.
Start by importing some packages that you'll need into the workspace,
%pylab inline
import numpy as np from scipy.interpolate import splprep, splev import matplotlib.pyplot as plt import mayavi.mlab as mplt from mpl_toolkits.mplot3d import Axes3D
Define a borehole path
We define the trajectory of a borehole, using a series of x, y, z points, and make each component of the borehole an array. If we had a real well, we load the numbers from the deviation survey just the same.
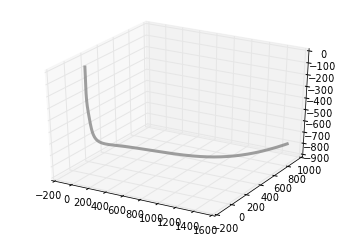
trajectory = np.array([[ 0, 0, 0],
[ 0, 0, -100],
[ 0, 0, -200],
[ 5, 0, -300],
[ 10, 10, -400],
[ 20, 20, -500],
[ 40, 80, -650],
[ 160, 160, -700],
[ 600, 400, -800],
[1500, 960, -800]])
x = trajectory[:,0]
y = trajectory[:,1]
z = trajectory[:,2]
But since we want the borehole to be continuous and smoothly shaped, we can up-sample the borehole by finding the B-spline representation of the well path,
smoothness = 3.0 spline_order = 3 nest = -1 # estimate of number of knots needed (-1 = maximal) knot_points, u = splprep([x,y,z], s=smoothness, k=spline_order, nest=-1) # Evaluate spline, including interpolated points x_int, y_int, z_int = splev(np.linspace(0, 1, 400), knot_points) plt.gca(projection='3d') plt.plot(x_int, y_int, z_int, color='grey', lw=3, alpha=0.75) plt.show()
Define frac ports
Let's define a completion program so that our wellbore has 6 frac stages,
number_of_fracs = 6
and let's make it so that each one emanates from equally spaced frac ports spanning the bottom two-thirds of the well.
x_frac, y_frac, z_frac = splev(np.linspace(0.33, 1, number_of_fracs), knot_points)
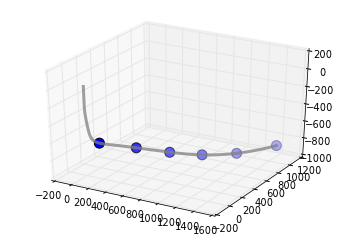 Make a set of 3D axes, so we can plot the well path and the frac ports.
Make a set of 3D axes, so we can plot the well path and the frac ports.
ax = plt.axes(projection='3d')
ax.plot(x_int, y_int, z_int, color='grey',
lw=3, alpha=0.75)
ax.scatter(x_frac, y_frac, z_frac,
s=100, c='grey')
plt.show()
Set a colour for each stage by cycling through red, green, and blue,
stage_color = []
for i in np.arange(number_of_fracs):
color = (1.0, 0.1, 0.1)
stage_color.append(np.roll(color, i))
stage_color = tuple(map(tuple, stage_color))
Define microseismic points
One approach is to create some dimensions for each frac stage and generate 100 points randomly within each zone. Each frac has an x half-length, y half-length, and z half-length. Let's also vary these randomly for each of the 6 stages. Define the dimensions for each stage:
frac_dims = []
half_extents = [500, 1000, 250]
for i in range(number_of_fracs):
for j in range(len(half_extents)):
dim = np.random.rand(3)[j] * half_extents[j]
frac_dims.append(dim)
frac_dims = np.reshape(frac_dims, (number_of_fracs, 3))
Plot microseismic point clouds with 100 points for each stage. The following code should launch a 3D viewer scene in its own window:
size_scalar = 100000
mplt.plot3d(x_int, y_int, z_int, tube_radius=10)
for i in range(number_of_fracs):
x_cloud = frac_dims[i,0] * (np.random.rand(100) - 0.5)
y_cloud = frac_dims[i,1] * (np.random.rand(100) - 0.5)
z_cloud = frac_dims[i,2] * (np.random.rand(100) - 0.5)
x_event = x_frac[i] + x_cloud
y_event = y_frac[i] + y_cloud
z_event = z_frac[i] + z_cloud
# Let's make the size of each point inversely proportional
# to the distance from the frac port
size = size_scalar / ((x_cloud**2 + y_cloud**2 + z_cloud**2)**0.002)
mplt.points3d(x_event, y_event, z_event, size, mode='sphere', colormap='jet')
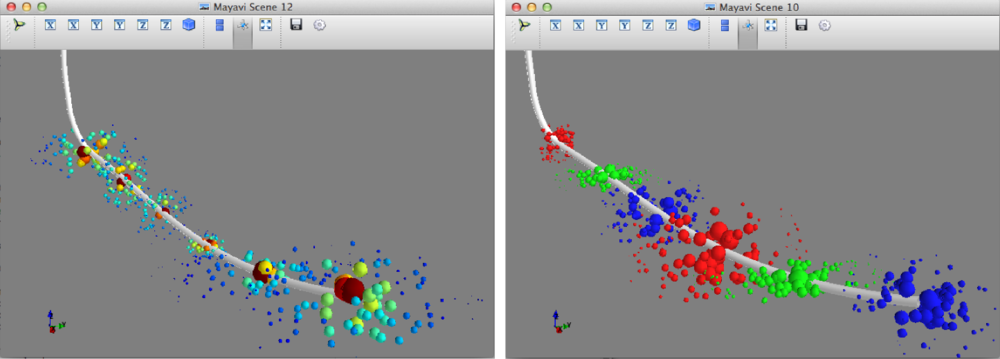
You can swap out the last line in the code block above with mplt.points3d(x_event, y_event, z_event, size, mode='sphere', color=stage_color[i]) to colour each event by its corresponding stage.
A day of geocomputing
I will be in Calgary in the new year and running a one-day version of this new course. To start building your own tools, pick a date and sign up:








 Except where noted, this content is licensed
Except where noted, this content is licensed