A really good conversation

Today was Day 2 of the Canada GeoConvention. But... all we had the energy for was the famous Unsolved Problems Unsession. So no real highlights today, just a report from the floor of Room 101.

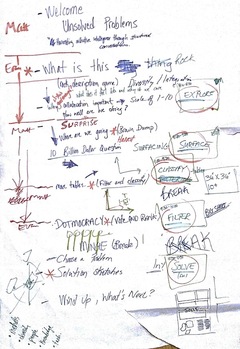Today was the day. We slept about as well as two 8-year-olds on Christmas Eve, having been up half the night obsessively micro-hacking our meeting design (right). The nervous anticipation was richly rewarded. About 50 of the most creative, inquisitive, daring geoscientists at the GeoConvention came to the Unsession — mostly on purpose. Together, the group surfaced over 100 pressing questions facing the upstream industry, then filtered this list to 4 wide-reaching problems of integration:

• making the industry more open
• coping with error and uncertainty
• improving seismic resolution
• improving the way our industry is perceived

We owe a massive debt of thanks to our heroic hosts: Greg Bennett, Tannis McCartney, Chris Chalcraft, Adrian Smith, Charlene Radons, Cale White, Jenson Tan, and Tooney Fink. Every one of them far exceeded their brief and brought 100× more clarity and continuity to the conversations than we could have had without them. Seriously awesome people.  

This process of waking our industry up to new ways of collaborating is just beginning. We will, you can be certain, write more about the unsession after we've had a little time to parse and digest what happened.

If you're at the conference, tell us what we missed today!

A revolution in seismic acquisition?

We're in warm, sunny Calgary for the GeoConvention 2013. The conference feels like it's really embracing geophysics this year — in the past it's always felt more geological somehow. Even the exhibition floor felt dominated by geophysics. Someone we spoke to speculated that companies were holding their geological cards close to their chests, but the service companies are still happy to talk about (ahem, promote) their geophysical advances.

Are you at the conference? What do you think? Let us know in the comments.

We caught about 15 talks of the 100 or so on offer today. A few of them ignited the old whines about half-cocked proofs of efficacy. Why is it still acceptable to say that a particular seismic volume or inversion result is 'higher resolution' or 'more geological' with nothing more than a couple of sections or timeslices as evidence?

People are excited about designing seismic acquisition expressly for wavefield reconstruction. In a whole session devoted to the subject, for example, Mauricio Sacchi showed how randomization helps with regularization in processing, allowing us to either get better image quality, or to lower cost. It feels like the start of a new wave of innovation in acquisition, which has more than its fair share of recent innovation: multi-component, wide azimuth, dual-sensor, simultaneous source...

Is it a revolution? Or just the fallacy of new things looking revolutionary... until the next new thing? It's intriguing to the non-specialist. People are talking about 'beyond Nyquist' again, but this time without inducing howls of derision. We just spent an hour talking about it, and we think there's something deep going on... we're just not sure how to articulate it yet.

Unsolved problems

We were at the conference today, but really we are focused on the session we're hosting tomorrow morning. Along with a roomful of adventurous conference-goers (you're invited too!), looking for the most pressing questions in subsurface science. We start at 8 a.m. in Telus 101/102 on the main floor of the north building.

What is an unsession?

Yesterday I invited you (yes, you) to our Unsolved Problems Unsession on 7 May in Calgary. What exactly will be involved? We think we can accomplish two things:

1. Brainstorm the top 10, or 20, or 50 most pressing problems in exploration geoscience today. Not limited to but focusing on those problems that affect how well we interface — with each other, with engineers, with financial people, with the public even. Integration problems.
2. Select one or two of those problems and solve them! Well, not solve them, but explore ways to approach solving them. What might a solution be worth? How many disciplines does it touch? How long might it take? Where could we start? Who can help?

There are bright, energetic young people out there looking for relevant problems to work on towards a Master's or PhD. There are entrepreneurs looking for high-value problems to create a new business from. And software companies looking for ways to be more useful and relevant to their users. And there is more than one interpreter wishing that innovation would speed up a bit in our industry and make their work a little — or a lot — easier. 

We don't know where it will lead, but we think this unsession is one way to get some conversations going. This is not a session to dip in and out of — we need 4 hours of your time. Bring your experience, your uniqueness, and your curiosity.

Let's reboot our imaginations about what we can do in our science.

An invitation to a brainstorm

Who of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries? What particular goals will there be toward which the leading [geoscientific] spirits of coming generations will strive? What new methods and new facts in the wide and rich field of [geoscientific] thought will the new centuries disclose?

— Adapted from David Hilbert (1902). Mathematical Problems, Bulletin of the American Mathematical Society 8 (10), p 437–479. Originally appeared in in Göttinger Nachrichten, 1900, pp. 253–297.

Back at the end of October, just before the SEG Annual Meeting, I did some whining about conferences: so many amazing, creative, energetic geoscientists, doing too much listening and not enough doing. The next day, I proposed some ways to make conferences for productive — for us as scientists, and for our science itself. 

Evan and I are chairing a new kind of session at the Calgary GeoConvention this year. What does ‘new kind of session’ mean? Here’s the lowdown:

The Unsolved Problems Unsession at the 2013 GeoConvention will transform conference attendees, normally little more than spectators, into active participants and collaborators. We are gathering 60 of the brightest, sparkiest minds in exploration geoscience to debate the open questions in our field, and create new approaches to solving them. The nearly 4-hour session will look, feel, and function unlike any other session at the conference. The outcome will be a list of real problems that affect our daily work as subsurface professionals — especially those in the hard-to-reach spots between our disciplines. Come and help shed some light, room 101, Tuesday 7 May, 8:00 till 11:45.

What you can do

• Where does your workflow stumble? Think up the most pressing unsolved problems in your workflows — especially ones that slow down collaboration between the disciplines. They might be organizational, they might be technological, they might be scientific.
• Put 7 May in your calendar and come to our session! Better yet, bring a friend. We can accommodate about 60 people. Be one of the first to experience a new kind of session!
• If you would like to help host the event, we're looking for 5 enthusiastic volunteers to play a slightly enlarged role, helping guide the brainstorming and capture the goodness. You know who you are. Email hello@agilegeoscience.com. 

Backwards and forwards reasoning

Most people, if you describe a train of events to them will tell you what the result will be. There will be few people however, that if you told them a result, would be able to evolve from their own consciousness what the steps were that led to that result. This is what I mean when I talk about reasoning backward.

— Sherlock Holmes, A Study in Scarlet, Sir Arthur Conan Doyle (1887)

Reasoning backwards is the process of solving an inverse problem — estimating a physical system from indirect data. Straight-up reasoning, which we call the forward problem, is a kind of data collection: empiricism. It obeys a natural causality by which we relate model parameters to the data that we observe.

Modeling a measurement

Where are you headed? Every subsurface problem can be expressed as the arrow between two or more such panels.Inverse problems exists for two reasons. We are incapable of measuring what we are actually interested in, and it is impossible to measure a subject in enough detail, and in all aspects that matter. If, for instance, I ask you to determine my weight, you will be troubled if the only tool I allow is a ruler. Even if you are incredibly accurate with your tool, at best, you can construct only an estimation of the desired quantity. This estimation of reality is what we call a model. The process of estimation is called inversion.

Measuring a model

Forward problems are ways in which we acquire information about natural phenomena. Given a model (me, say), it is easy to measure some property (my height, say) accurately and precisely. But given my height as the starting point, it is impossible to estimate the me from which it came. This is an example of an ill-posed problem. In this case, there is an infinite number of models that share my measurements, though each model is described by one exact solution. 

Solving forward problems are nessecary to determine if a model fits a set of observations. So you'd expect it to be performed as a routine compliment to interpretation; a way to validate our assumptions, and train our intuition.  

The math of reasoning

Forward and inverse problems can be cast in this seemingly simple equation.

where d is a vector containing N observations (the data), m is a vector of M model parameters (the model), and G is a N × M matrix operator that connects the two. The structure of G changes depending on the problem, but it is where 'the experiment' goes. Given a set of model parameters m, the forward problem is to predict the data d produced by the experiment. This is as simple as plugging values into a system of equations. The inverse problem is much more difficult: given a set of observations d, estimate the model parameters m.

I think interpreters should describe their work within the Gm = d framework. Doing so would safeguard against mixing up observations, which should be objective, and interpretations, which contain assumptions. Know the difference between m and d. Express it with an arrow on a diagram if you like, to make it clear which direction you are heading in.

Illustrations for this post were created using data from the Marmousi synthetic seismic data set. The blue seismic trace and its corresponding velocity profile is at location no. 250.

How to get paid big bucks

Yesterday I asked 'What is inversion?' and started looking at problems in geoscience as either forward problems or inverse problems. So what are some examples of inverse problems in geoscience? Reversing our forward problem examples:

• Given a suite of sedimentological observations, provide the depositional environment. This is a hard problem, because different environments can produce similar-looking facies. It is ill-conditioned, because small changes in the input (e.g. the presence of glaucony, or Cylindrichnus) produces large changes in the interpretation.
• Given a seismic trace, produce an impedance log. Without a wavelet, we cannot uniquely deduce the impedance log — there are infinitely many combinations of log and wavelet that will give rise to the same seismic trace. This is the challenge of seismic inversion. 

To solve these problems, we must use induction — a fancy name for informed guesswork. For example, we can use judgement about likely wavelets, or the expected geology, to constrain the geophysical problem and reduce the number of possibilities. This, as they say, is why we're paid the big bucks. Indeed, perhaps we can generalize: people who are paid big bucks are solving inverse problems...

• How do we balance the budget?
• What combination of chemicals might cure pancreatic cancer?
• What musical score would best complement this screenplay?
• How do I act to portray a grief-stricken war veteran who loves ballet?

What was the last inverse problem you solved?

Update on 2013-04-17 21:50 by Matt Hall

Moar inversion! Don't miss the previous post in this mini-series, or the next one — where things get a bit more mathy. 

What is inversion?

Inverse problems are at the heart of geoscience. But I only hear hardcore geophysicists talk about them. Maybe this is because they're hard problems to solve, requiring mathematical rigour and computational clout. But the language is useful, and the realization that some problems are just damn hard — unsolvable, even — is actually kind of liberating. 

Forwards first

Before worrying about inverse problems, it helps to understand what a forward problem is. A forward problem starts with plenty of inputs, and asks for a straightforward, algorithmic, computable output. For example:

• What is 4 × 5?
• Given a depositional environment, what sedimentological features do we expect?
• Given an impedance log and a wavelet, compute a synthetic seismogram.

These problems are solved by deductive reasoning, and have outcomes that are no less certain than the inputs.

Can you do it backwards?

You can guess what an inverse problem looks like. Computing 4 × 5 was pretty easy, even for a geophysicist, but it's not only difficult to do it backwards, it's impossible:

20 = what × what

You can solve it easily enough, but solutions are, to use the jargon, non-unique: 2 × 10, 7.2 × 1.666..., 6.3662 × π — you get the idea. One way to deal with such under-determined systems of equations is to know about, or guess, some constraints. For example, perhaps our system — our model — only includes integers. That narrows it down to three solutions. If we also know that the integers are less than 10, there can be only one solution.

Non-uniqueness is a characteristic of ill-posed problems. Ill-posedness is a dead giveaway of an inverse problem. Proposed by Jacques Hadamard, the concept is the opposite of well-posedness, which has three criteria:

• A solution exists.
• The solution is unique.
• The solution is well-conditioned, which means it doesn't change disproportionately when the input changes. 

Notice the way the example problem was presented: one equation, two unknowns. There is already a priori knowledge about the system: there are two numbers, and the operator is multiplication. In geoscience, since the earth is not a computer, we depend on such knowledge about the nature of the system — what the variables are, how they interact, etc. We are always working with a model of nature.

Tomorrow, I'll look at some specific examples of inverse problems, and Evan will continue the conversation next week.

Update on 2013-04-12 11:18 by Matt Hall

Don't miss the first follow-up to this article, How to get paid big bucks. 

The calculus of geology

Calculus is the tool for studying things that change. Even so, in the midst of the dynamic and heterogeneous earth, calculus is an under-practised and, around the water-cooler at least, under-celebrated workhorse. Maybe that's because people don't realize it's all around us. Let's change that. 

Derivatives of duration

We can plot the time f(x) that passes as a seismic wave travels though space x. This function is known to many geophysicists as the time-to-depth function. It is key for converting borehole measurements, effectively recorded using a measuring tape, to seismic measurements, recorded using a stop watch.

Now let's take the derivative of f(x) with repsect to x. The result is the slowness function (the reciprocal of interval velocity):

The time duration that a seismic wave travels over a small interval (one metre). This function is an actual sonic well log. Differentiating once again yields this curious spiky function:

Geophysicists will spot that this resembles a reflection coefficient series, which governs seismic amplitudes. This is actually a transmission coefficient function, but that small detail is beside the point. In this example, the creating a synthetic seismogram mimics the calculus of geology. 

If you are familiar with the integrated trace attribute, you will recognize that it is an attempt to compute geology by integrating reflectivity spikes. The only issue in this case, and it is a major issue, is that the seismic trace is bandlimited. It does not contain all the information about the earth's slowness. So the earth's geology remains elusive and blurry.

The derivative of slowness yields the reflection boundaries, the integral of slowness yields their position. So in geophysics speak, I wonder, is forward modeling akin to differentiation, and inverse modeling akin to integration? I find it fascinating that these three functions have essentially the same density of information, yet they look increasingly complicated when we take derivatives. 

What other functions do you come across that might benefit from the calculus treatment?

The sonic log used in this example is from the O-32-B/11-E-64 well onshore Nova Scotia, which is publically available but not easily accessible online.

Review: The Wave Watcher's Companion

Visit Amazon.com

The Wave Watcher's Companion: From Ocean Waves to Light Waves via Shock Waves, Stadium Waves, and All the Rest of Life's Undulations
Gavin Pretor-Pinney, Perigee (USA), Bloomsbury (UK), July 2010, $22.95

This book was on my reading list, and then on my shelf, for ages. Now I wish I'd snapped it up and read it immediately. In my defence, the end of 2010 was a busy time for me, what with turning my career upside down and everything, but I'm sure there's a lesson there somewhere...

If you think of yourself as a geophysicist, stop reading this review and buy this book immediately. 

OK, now they've gone, we can look more closely. Gavin Pretor-Pinney is the chap behind The Cloud Appreciation Society, the author of The Cloudspotter's Guide, and co-creator of The Idler Magazine. He not a scientist, but a witty writer with a high curiosity index. The book reads like an extended blog post, or a chat in the pub. A really geeky chat. 

Geophysicists are naturally drawn to all things wavy, but the book touches on sedimentology too — from dunes to tsunamis to seiches. Indeed, the author prods at some interesting questions about what exactly waves are, and whether bedforms like dunes (right) qualify as waves or not. According to Andreas Baas, "it all depends on how loose is your definition of a wave." Pretor-Pinney likes to connect all possible dots, so he settles for a loose definition, backing it up with comparisons to tanks and traffic jams. 

The most eye-opening part for me was Chapter 6, The Fifth Wave, about shock waves. I never knew that there's a whole class of waves that don't obey the normal rules of wave motion: they don't obey the speed limits, they don't reflect or refract properly, and they can't even be bothered to interfere like normal (that is, linear) waves. Just one of those moments when you realize that everything you think you know is actually a gross simplification. I love those moments.

The book is a little light on explanation. Quite a few of the more interesting parts end a little abruptly with something like, "weird, huh?". But there are plenty of notes for keeners to follow up on, and the upside is the jaunty pace and adventurous mix of examples. This one goes on my 're-read some day' shelf. (I don't re-read books, but it's the thought that counts).

Figure excerpt from Pretor-Pinney's book, copyright of the author and Penguin Publishing USA. Considered fair use.

Interpreting spectral gamma-ray logs

Before you can start interpreting spectral gamma-ray logs (or, indeed, any kind of data), you need to ask about quality.

Calibrate your tool...

The main issues affecting the quality of the logs are tool calibration and drilling mud composition. I think there's a tendency to assume that delivered logs have been rigorously quality checked, but... they haven't. The only safe assumption is that nobody cares about your logs as much as you. (There is a huge opportunity for service companies here — but in my experience they tend to be focused on speed and quantity, not quality.)

Calibration is critical. The measurement device in the tool consists of a thallium-laced NaI crystal and a photomultiplier. Both of these components are sensitive to temperature, so calibration is especially important when the temperature of the tool is changing often. If the surface temperature is very different from the downhole—winter in Canada—calibrate often.

Drilling mud containing KCl (to improve borehole stability) increases the apparent potassium content of the formation, while barite acts as a gamma-ray absorber and reduces the count rates, especially in the low energies (potassium).

One of the key quality control indicators is negative readings on the uranium log. A few negative values are normal, but many zero-crossings may indicate that the tool was improperly calibrated. It is imperative to quality control all of the logs, for bad readings and pick-up effects, before doing any quantitative work.

...and your interpretation

Most interpretations of spectral-gamma ray logs focus on the relationships between the three elemental concentrations. In particular, Th/K and Th/U are often used for petrophysical interpretation and log correlation. In calculating these ratios, Schlumberger uses the following cut-offs: if uranium < 0.5 then uranium = 0.5; if potassium < 0.004 then potassium = 0.001 (according to my reference manual for the natural gamma tool).

In general, high K values may be caused by the presence of potassium feldspars or micas. Glauconite usually produces a spike in the K log. High Th values may be associated with the presence of heavy minerals, particularly in channel deposits. Increased Th values may also be associated with an increased input of terrigenous clays. Increases in U are frequently associated with the presence of organic matter. For example, according to the ODP, particularly high U concentrations (> 5 ppm) and low Th/U ratios (< 2) often occur in black shale deposits.

The logs here, from Kansas Geological Survey open file 90-27 by Macfarlane et al. shows a quite overt interpretive approach, with the Th/K log labelled with minerals (feldspar, mica, illite–smectite) and the Th/U log in uranium 'fixedness', a proxy for organic matter.

Sounds useful. But really, you can probably find just a paper to support just about any interpretation you want to make. Which isn't to say that spectral gamma-ray is no use — it's just not diagnostic on its own. You need to calibrate it to your own basin and your own stratigraphy. This means careful, preferably quantitative, comparison of core and logs. 

Further reading 

• Ross Crain's Petrophysical Handbook is a mine of well logging goodness
• Paul Glover's MSc course notes are very comprehensive on most well logging topics
• Fabricius et al. (2003). Geological Survey of Denmark and Greenland Bulletin 1, 349–366. A case stuudy from the Danish Central Graben.