x lines of Python: Physical units
/Difficulty rating: Intermediate
Have you ever wished you could carry units around with your quantities — and have the computer figure out the best units and multipliers to use?
pint is a nice, compact library for doing just this, handling all your dimensional analysis needs. It can also detect units from strings. We can define our own units, it knows about multipliers (kilo, mega, etc), and it even works with numpy and pandas.
To use it in its typical mode, we import the library then instantiate a UnitRegistry object. The registry contains lots of physical units:
import pint units = pint.UnitRegistry() thickness = 68 * units.m
Now thickness is a Quantity object with the value <Quantity(68, 'meter')>, but in Jupyter we see a nice 68 meter (as far as I know, you're stuck with US spelling).
Let's make another quantity and multiply the two:
area = 60 * units.km**2 volume = thickness * area
This results in volume having the value <Quantity(4080, 'kilometer ** 2 * meter')>, which pint can convert to any units you like, as long as they are compatible:
>>> volume.to('pint') 8622575788969.967 pint
More conveniently still, you can ask for 'compact' units. For example, volume.to_compact('pint') returns 8.622575788969966 terapint. (I guess that's why we don't use pints for field volumes!)
There are lots and lots of other things you can do with pint; some of them — dealing with specialist units, NumPy arrays, and Pandas dataframes — are demonstrated in the Notebook accompanying this post. You can use one of these links to run this right now in your browser if you like:
Run the accompanying notebook in MyBinder
Run the notebook in Google Colaboratory (note the install cell at the beginning)
That's it for pint. I hope you enjoy using it in your scientific computing projects. If you have your own tips for handling units in Python, let us know in the comments!
There are some other options for handling units in Python:
quantities, which handles uncertainties without also needing theuncertaintiespackage.astropy.units, part of the largeastropyproject, is popular among physicists.










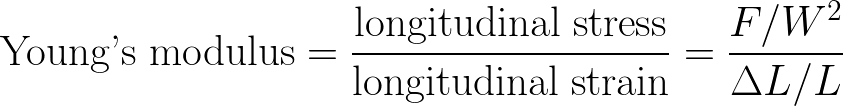












 Except where noted, this content is licensed
Except where noted, this content is licensed