What changes sea-level?

Relative sea-level is complicated. It is measured from some fixed point in the sediment pile, not a fixed point in the earth. So if, for example, global sea-level (eustasy) stays constant but there is local subsidence at a fault, say, then we can say that relative sea-level has increased. Another common cause is isostatic rebound during interglacials, causing a fall in relative sea-level and a seaward regression of the coastline. Because the system didn't build out into the sea by itself, this is sometimes called a forced regression. Here's a nice example of a raised beach formed this way, from Langerstone Point, near Prawle in Devon, UK:

Image: Tony Atkin, licensed under CC-BY-SA-2.0. From Wikimedia Commons. 

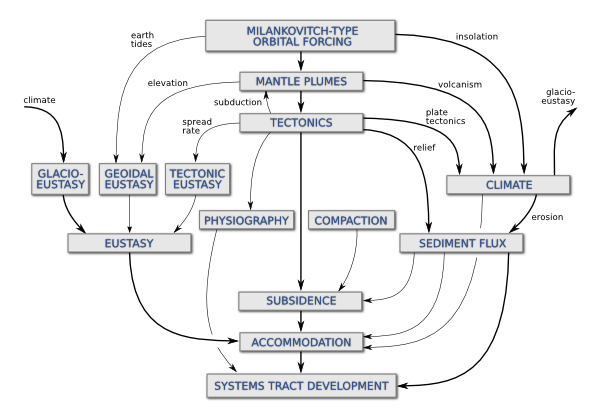
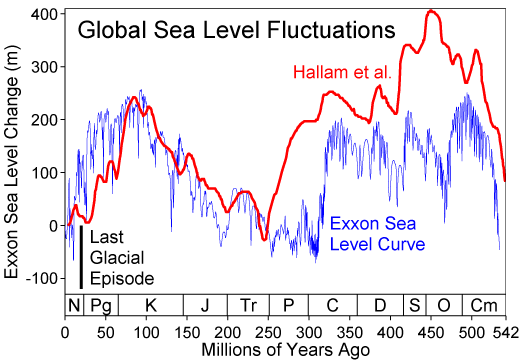
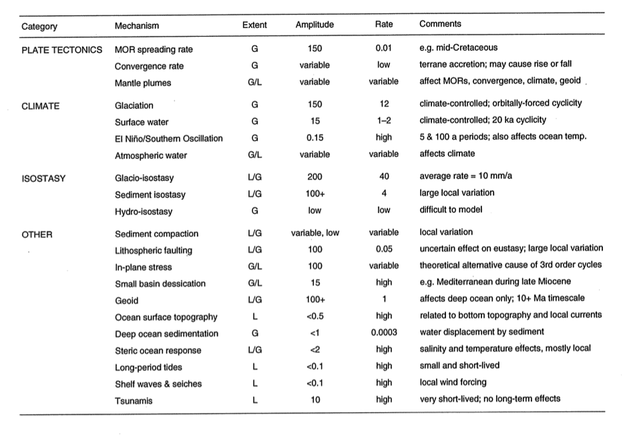
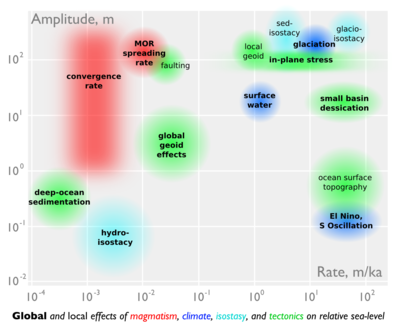
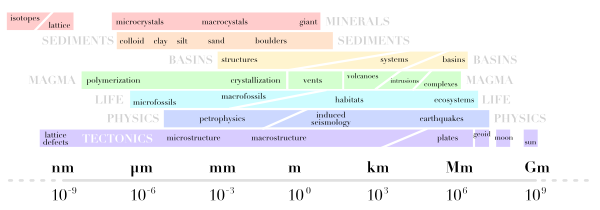
Two weeks ago I wrote about some of the factors affecting relative sea-level, and the scales on which those processes operate. Before that, I had mentioned my undergraduate fascination with Milankovitch cyclicity and its influence on a range of geological processes. Complexity and interaction were favourite subjects of mine, and I built on this a bit in my graduate studies. To try to visualize some of the connectedness of the controls on sea-level, I drew a geophantasmagram that I still refer to occasionally:

Accommodation refers to the underwater space available for sediment deposition; it is closely related to relative sea-level. The end of the story, at least as far as gross stratigraphy is concerned, is the development of stratigraphic package, like a shelf-edge delta or a submarine fan. Systems tracts is just a jargon term for these packages when they are explicitly related to changes in relative sea-level. 

I am drawn to making diagrams like this; I like mind-maps and other network-like graphs. They help me think about complex systems. But I'm not sure they always help anyone other than the creator; I know I find others' efforts harder to read than my own. But if you have suggestions or improvements to offer, I'd love to hear from you.

Shattering shale

In shale gas exploration, one of the most slippery attributes we are interested in is fracability. The problem is that the rocks we study have different compositions and burial histories, so it's hard to pin down the relative roles of intrinsic rock properties and extrinsic stress states. Glass could be considered an end member for brittleness, and it has fairly uniform elastic parameters and bulk composition (it's amorphous silica). Perhaps we can learn something about the role of stresses by looking more closely at how glass fractures. 

The mechanics of glass can be characterized by two aspects: how it's made, and how it breaks.

Annealed glass is made by pouring molten glass onto a thin sheet of tin. Upon contact, the tin melts allowing for two perfectly smooth and parallel surfaces. The glass is cooled slowly so that stress irregularities dissipate evenly throughout, reducing local weak points. This is ordinary glass, as you might find in a mirror.

Tempered glass is made by heating annealed glass to near its softening point, about 720˚C, and then quickly cooling it by quenching with air jets. The exterior surface shrinks, freezing it into compression, while the soft interior of the glass gets pulled out by tensional forces as it freezes (diagram). 

How glass is made is directly linked to how it breaks. Annealed glass is weaker, and breaks into sparse splinters. The surface of tempered glass is stronger, and when it breaks, it breaks catastrophically; the interior tensional energy releases cracks from the inside out.

A piece of tempered glass is 4-6 times stronger than a piece of annealed glass with the same elastic properties, composition, density and dimensions. This means it looks almost identical but requires much more stress to break. Visually and empirically, it is not easy to tell the difference between annealed and tempered glass. But when you break it, the difference is obvious. So here, for two very brittle materials, with all else being equal, the stress state plays the dominant role in determining the mode of failure.

Because natural permeability is so low in fine grained rocks, production companies induce artificial fractures to connect flow pathways to the wellbore. The more surface area exposed, the more methane will be liberated.

If we are trying to fracture-stimulate shale to get at the molecules trapped inside, we would clearly prefer shale that shatters like tempered glass. The big question is: how do we explore for shale like this?

One approach is to isolate parameters such as natural fractures, anisotropy, pore pressure, composition, and organic content and study their independent effects. In upcoming posts, we'll explore the tools and techniques for measuring these parameters across scale space for characterizing fracability. 

Update on 2011-04-19 15:59 by Matt Hall

You might also like some of our other recent posts about shale gas:

• What is shale?, a look at how to define shale
• Shale vs tight, a comparison with tight gas plays
• What is unconventional?, a look at how to define unconventional resources

Scales of sea-level change

Click to read about sea level on Wikipedia. Image prepared by Robert Rohde and licensed for public use under CC-BY-SA.Sea level changes. It changes all the time, and always has (right). It's well known, and obvious, that levels of glaciation, especially at the polar ice-caps, are important controls on the rate and magnitude of changes in global sea level. Less intuitively, lots of other effects can play a part: changes in mid-ocean ridge spreading rates, the changing shape of the geoid, and local tectonics.

A recent paper in Science by Petersen et al (2010) showed evidence for mantle plumes driving the cyclicity of sedimentary sequences. This would be a fairly local effect, on the order of tens to hundreds of kilometres. This is important because some geologists believe in the global correlatability of these sequences. A fanciful belief in my view—but that's another story.

The paper reminded me of an attempt I once made to catalog the controls on sea level, from long-term global effects like greenhouse–icehouse periods, to short-term local effects like fault movement. I made the table below. I think most of the data, perhaps all of it, were from Emery and Aubrey (1991). It's hard to admit, because I don't feel that old, but this is a rather dated publication now; I think it's solid enough for the sort of high-level overview I am interested in. 

After last week's doodling, the table inspired me to try another scale-space cartoon. I put amplitude on the y-axis, rate on the x-axis. Effects with global reach are in bold, those that are dominantly local are not. The rather lurid colours represent different domains: magmatic, climatic, isostatic, and (in green) 'other'. The categories and the data correspond to the table.
It is interesting how many processes are competing for that top right-hand corner: rapid, high-amplitude sea level change. Clearly, those are the processes we care about most as sequence stratigraphers, but also as a society struggling with the consequences of our energy addiction.

References
Emery, K & D Aubrey (1991). Sea-levels, land levels and tide gauges. Springer-Verlag, New York, 237p.
Petersen, K, S Nielsen, O Clausen, R Stephenson & T Gerya (2010). Small-scale mantle convection produces stratigraphic sequences in sedimentary basins. Science 329 (5993) p 827–830, August 2010. DOI: 10.1126/science.1190115

The scales of geoscience

Helicopter at Mount St Helens in 2007. Image: USGS.Geoscientists' brains are necessarily helicoptery. They can quickly climb and descend, hover or fly. This ability to zoom in and out, changing scale and range, develops with experience. Thinking and talking about scales, especially those outside your usual realm of thought, are good ways to develop your aptitude and intuition. Intuition especially is bound to the realms of your experience: millimetres to kilometres, seconds to decades. 

Being helicoptery is important because processes can manifest themselves in different ways at different scales. Currents, for example, can result in sorting and rounding of grains, but you can often only see this with a hand-lens (unless the grains are automobiles). The same environment might produce ripples at the centimetre scale, dunes at the decametre scale, channels at the kilometre scale, and an entire fluvial basin at another couple of orders of magnitude beyond that. In moments of true clarity, a geologist might think across 10 or 15 orders of magnitude in one thought, perhaps even more.

A couple of years ago, the brilliant web comic artist xkcd drew a couple of beautiful infographics depicting scale. Entitled height and depth (left), they showed the entire universe in a logarithmic scale space. More recently, a couple of amazing visualizations have offered different visions of the same theme: the wonderful Scale of the Universe, which looks at spatial scale, and the utterly magic ChronoZoom, which does a similar thing with geologic time. Wonderful.

These creations inspired me to try to map geological disciplines onto scale space. You can see how I did below. I do like the idea but I am not very keen on my execution. I think I will add a time dimension and have another go, but I thought I'd share it at this stage. I might even try drawing the next one freehand, but I ain't no Randall Munroe.

I'd be very happy to receive any feedback about improving this, or please post your own attempts!

Update on 2011-04-13 03:12 by Matt Hall

I have just finished a new version of this graphic, incorporating some comments from readers. I replaced the one in the original post, so please grab it from there if you want to see what I did. 

If you like this post, you might also like the more recent one on the scales of relative sea-level change, and also this older one on the scales of various experiments in oil & gas geoscience. 

Great geophysicists #3

Today is a historic day for greatness: Rene Descartes was born exactly 415 years ago, and Isaac Newton died 284 years ago. They both contributed to our understanding of physical phenomena and the natural world and, while not exactly geophysicists, they changed how scientists think about waves in general, and light in particular.

Unweaving the rainbow

Scientists of the day recognized two types of colour. Apparent colours were those seen in prisms and rainbows, where light itself was refracted into colours. Real colours, on the other hand, were a property of bodies, disclosed by light but not produced by that light. Descartes studied refraction in raindrops and helped propagate Snell’s law in his 1637 paper, Dioptrica. His work severed this apparent–real dichotomy: all colours are apparent, and the colour of an object depends on the light you shine on it.

Newton began to work seriously with crystalline prisms around 1666. He was the first to demonstrate that white light is a scrambled superposition of wavelengths; a visual cacophony of information. Not only does a ray bend in relation to the wave speed of the material it is entering (read the post on Snellius), but Newton made one more connection. The intrinsic wave speed of the material, in turn depends on the frequency of the wave. This phenomenon is known as dispersion; different frequency components are slowed by different amounts, angling onto different paths.

What does all this mean for seismic data?

Seismic pulses, which strut and fret through the earth, reflecting and transmitting through its myriad contrasts, make for a more complicated type of prism-dispersion experiment. Compared to visible light, the effects of dispersion are subtle, negligible even, in the seismic band 2–200 Hz. However, we may measure a rock to have a wave speed of 3000 m/s at 50 Hz, and 3500 m/s at 20 kHz (logging frequencies), and 4000 m/s at 10 MHz (core laboratory frequencies). On one hand, this should be incredibly disconcerting for subsurface scientists: it keeps us from bridging the integration gap empirically. It is also a reason why geophysicists get away with haphazardly stretching and squeezing travel time measurements taken at different scales to tie wells to seismic. Is dispersion the interpreters’ fudge-factor when our multi-scale data don’t corroborate?

Chris Liner, blogging at Seismos, points out

...so much of classical seismology and wave theory is nondispersive: basic theory of P and S waves, Rayleigh waves in a half-space, geometric spreading, reflection and transmission coefficients, head waves, etc. Yet when we look at real data, strong dispersion abounds. The development of spectral decomposition has served to highlight this fact.

We should think about studying dispersion more, not just as a nuisance for what is lost (as it has been traditionally viewed), but as a colourful, scale-dependant property of the earth whose stories we seek to hear.

D is for Domain

Domain is a term used to describe a variable for which a set of functions or signals are defined.

Time-domain describes functions or signals that change over time; depth-domain describes functions or signal that change over space. The oscillioscope, geophone, and heartrate monitor are tools used to visualize real-world signals in the time domain. The map, photograph, and well log are tools to describe signals in the depth (spatial) domain.

Because seismic waves are recorded in time (jargon: time series), seismic data are naturally presented and interpreted with time as the z-axis. Routinely though, geoscientists must convert data and data objects between the time and depth domain.

Consider the top of a hydrocarbon-bearing reservoir in the time domain (top panel). In this domain, it looks like wells A and B will hit the reservoir at the same elevation and encounter the same amount of pay.

In this example the velocities that enable domain conversion vary from left to right, thereby changing the position of this structure in depth. The velocity model (second panel) linearly decreases from 4000 m/s on the left, to 3500 m/s on the right; this equates to a 12.5% variation in the average velocities in the overburden above the reservoir.

This velocity gradient yields a depth image that is significantly different than the time domain representation. The symmetric time structure bump has been rotated and the spill point shifted from the left side to the right. More importantly, the amount of reservoir underneath the trap has been drastically reduced. 

Have you encountered examples in your work where data domains have been misleading?

Although it is perhaps more intuitive to work with depth-domain data wherever possible, sometimes there are good reasons to work with time. Excessive velocity uncertainty makes depth conversion so ambiguous that you are better off in time-domain. Time-domain signals are recorded at regular sample rates, which is better for signal processing and seismic attributes. Additionally, travel-time itself is an attribute in that it may be recorded or mapped for its physical meaning in some cases, for example time-lapse seismic.

If you think about it, all three of these models are in fact different representations of the same earth. It might be tempting to regard the depth picture as 'reality' but if it's your only perspective, you're kidding yourself. 

The etiology of rivers

The Ordovician was a primitive time. No mammals. No birds. No flowers. Most geologists know this, right? How about this: No meandering rivers.

Recently several geo-bloggers wrote about geological surprises. This was on my shortlist. 

A couple of weeks ago, Evan posted the story of scale-free gravity deformation we heard from Adrian Park and his collaborators at the Atlantic Geological Society's annual Colloquium. My own favourite from the conference was Neil Davies' account of the evolution of river systems:

Davies, Neil & Martin Gibling (2011). Pennsylvanian emergence of anabranching fluvial deposits: the parallel rise of arborescent vegetation and fixed-channel floodplains.

Neil, a post-doctoral researcher at Dalhousie University in Nova Scotia, Canada, started with a literature review. He read dozens of case studies of fluvial geology from all over the world, noting the interpretation of river morphology (fluvotype?). What he found was, to me at least, surprising: there were no reported meandering rivers before the Devonian, and no anabranching rivers before the Carboniferous. 

The idea that rivers have evolved over time, becoming more diverse and complex, is fascinating. At first glance, rivers might seem to be independent of life and other manifestly time-bound phenomena. But if we have learned only one thing in the last couple of decades, it is that the earth's systems are much more intimately related than this, and that life leaves its fingerprint on everything on earth's surface. 

A little terminology: anastomosing, a term I was more familiar with, is not strictly the correct term for these many-branched, fixed-channel rivers. Sedimentologists prefers anabranching. Braided and meandering river types are perhaps more familiar. The fluviotypes I'm showing here might be thought of as end members — most rivers show all of these characteristics through time and space.

What is the cause of this evolution? Davies and Gibling discussed two parallel effects: bank stabilization by soil and roots, and river diversion, technically called avulsion, by fallen trees. The first idea is straightforward: plants colonize river banks and floodplains, thus changing their susceptibility to erosion. The second idea was new to me, but is also simple: as trees got taller, it became more and more likely that fallen trunks would, with time, make avulsion more likely. 

There is another river type we are familiar with in Canada: the string of beaver dams (like this example from near Fort McMurray, Alberta). I don't know for sure, but I bet these first appeared in the Eocene. I have heard that the beaver is second only to man in terms of the magnitude of its effect on the environment. As usual, I suspect that microbes were not considered in this assertion.

All of this makes me wonder: are there other examples of evolution expressing itself in geomorphology like this?

Many thanks to Neil and Martin for allowing us to share this story. Please forgive my deliberate vagueness with some of the details — this work is not yet published; I will post a link to their forthcoming paper when it is published. The science and the data are theirs, any errors or inconsistencies are mine alone. 

Update on 2011-08-23 11:40 by Matt Hall

Davies and Gibling went on to publish this research in Nature Geoscience in August 2011.

The BBC covered the story in their science pages. 

How to cheat

Yesterday I posted the rock physics cheatsheet, which is a condensed version of useful seismic reservoir characterization and rock mechanics concepts. It's cheat as in simplify, not cheat as in swindle. 

As Matt discussed on Friday, heuristics can be shortcuts to hone your intuition. Our minds search to use rules of thumb to visualise the invisible and to solve sticky problems. That's where the cheat sheet comes in. You might not find rock physics that intuitive, but let's take a look at the table to see how it reveals some deeper patterns.

The table of elastic parameters is setup based on the fundamental notion that, if you have any two elastic properties previously defined, you can compute all the others. This is a consequence of one of the oldest laws in classical mechanics: Newton's second law, F=ma. In particular one thing I find profound about seismic velocity is that it is wholly determined by a ratio of competing tensional (elastic) forces to inertial (density) forces. To me, it is not immediately obvious that speed, with units of m/s, results from the ratio of pressure to density. 

This simple little equation has had a profound impact on the utility of seismology to the oil and gas industry. It links extrinsic dynamic properties (V_P) to intrinsic rock properties (K, μ, ρ). The goal of course, is not just to investigate elastic properties for the sake of it, but to link elastic properties to reservoir and petrophysical properties. This is traditionally done using a rock physics template. The one I find easiest to understand is the V_P/V_S vs P-impedance template, an example of which is shown on the cheatsheet. You will see others in use, for instance Bill Goodway has pioneered the λρ vs μρ (LMR) template.

In an upcoming post we'll look to deepen the connection between Newtonian mechanics and reservoir characterization.