Fitting a model to data

In studying the earth, we can't afford to take enough observations, and they will never be free of noise. So if you say you do geoscience, I hereby challenge you to formulate your work as a mathematical inverse problem. Inversion is a question: given the data, the physical equations, and details of the experiment, what is the distribution of physical properties? To answer this question we must address three more fundamental ones (Scales, Smith, and Treitel, 2001):

• How accurate is the data? Or what does fit mean?
• How accurately can we model the response of the system? Have we included all the physics that can contribute signifcantly to the data?
• What is known about the system independent of the data? There must be a systematic procedure for rejecting unreasonable models that fit the data as well.

Setting up an inverse problem means coming up with the equations that contain the physics and geometry of the system under study. The method for solving it depends on the nature of the system of equations. The simplest is the minimum norm solution, and you've heard of it before, but perhaps under a different name.

To fit is to optimize a system of equations

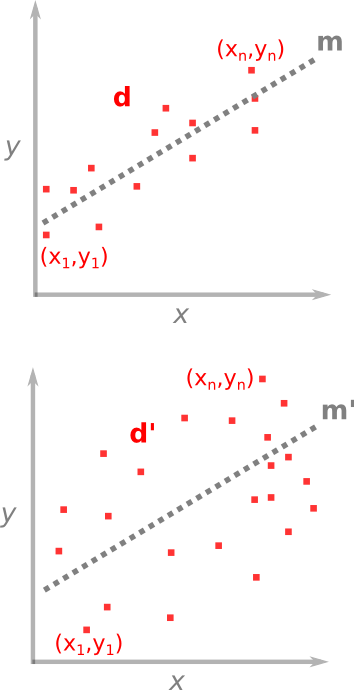For problems where the number of observations is greater than the number of unknowns, we want to find which unknowns fit the best. One case you're already familiar with is the method of least squares — you've used it fitting a line of through a set of points. A line is unambiguously described by only two parameters: slope a and y-axis intercept b. These are the unknowns in the problem, they are the model m that we wish to solve for. The problem of line-fitting through a set of points can be written out like this,

As I described in a previous post, the system of the problem takes the form d = Gm, where each row links a data point to an equation of a line. The model vector m (M × 1), is smaller than the data d (N × 1) which makes it an over-determined problem, and G is a N × M matrix holding the equations of the system.

Why cast a system of equations in this matrix form? Well, it turns out that the the best-fit line is precisely,

which are trivial matrix operations, once you've written out G.  T means to take the transpose, and –1 means the inverse, the rest is matrix multiplication. Another name for this is the minimum norm solution, because it defines the model parameters (slope and intercept) for which the lengths (vector norm) between the data and the model are a minimum. 

One benefit that comes from estimating a best-fit model is that you get the goodness-of-fit for free. Which is convenient because making sense of the earth doesn't just mean coming up with models, but also expressing their uncertainty, in terms of the errors with which they are linked.

I submit to you that every problem in geology can be formulated as a mathematical inverse problem. The benefit of doing so is not just to do math for math's sake, but it is only through quantitatively portraying ambiguous inferences and parameterizing non-uniqueness that we can do better than interpreting or guessing. 

Reference (well worth reading!)

Scales, JA, Smith, ML, and Treitel, S (2001). Introductory Geophysical Inverse Theory. Golden, Colorado: Samizdat Press. 

Laying it all out at the Core Conference

Bobbing in the wake of the talks, the Core Conference turned out to be more exemplary of this year's theme, Integration. Best of all were SAGD case studies, where multi-disciplinary experiments are the only way to make sense of the sticky stuff.

Coring through steam

Travis Shackleton from Cenovus did a wonderful presentation showing the impact of bioturbation, facies boundaries, and sedimentary structures on steam chamber evolution in the McMurray Formation at the FCCL project. And because I had the chance to work on this project with ConocoPhillips a few years ago, but didn't, this work induced both jealousy and awe. Their experiment design is best framed as a series of questions:

• What if we drilled, logged, and instrumented two wells only 10 m apart? (Awesome.)
• What if we collected core in both of them? (Double awesome.)
• What if the wells were in the middle of a mature steam chamber? (Triple awesome.)
• What if we collected 3D seismic after injecting all this steam and compare with with a 3D from before? (Quadruple awesome.)

It is the first public display of SAGD-depleted oil sand, made available by an innovation of high-temperature core recovery. Travis pointed to a portion of core that had been rinsed by more than 5 years of steam circulating through it. It had a pale brown color and a residual oil saturation S_O of 15% (bottom sample in the figure). Then he pointed to a segment of core above the top of the steam chamber. It too was depleted, by essentially the same amount. You'd never know just by looking. It was sticky and black and largely unscathed. My eyes were fooled, direct observation deceived.

A bitumen core full of fractures

Jen-Russel-Houston held up a half-tube of core of high-density fractures riddled throughout bitumen saturated rock. The behemoth oil sands that require thermal recovery assistance have an equally promising but lesser known carbonate cousin, still in its infancy. It is the bitumen saturated Grosmont Formation, located to the west of the more mature in-situ projects in sand. The reservoir is entirely dolomite, hosting its own unique structures affecting the spreading of steam and the reduction of bitumen's viscosity to a flowable level.

Jen and her team at OSUM hope their pilot will demonstrate that these fractures serve as transport channels for the steam, allowing it to creep around tight spots in the reservoir, which would otherwise be block the steam in its tracks. These are not the same troubling baffles and barriers caused by mud plugs or IHS, but permeability heterogeneities caused by the dolomitization process. A big question is the effective permeability at the length scales of production, which is phenomenologically different to measurements made from cut core. I overheard a spectator suggest to Jen that she try to freeze a sleeve of core, soak it with acid then rinse the dolomite out the bottom. After which only a frozen sculpture of the bitumen would remain. Crazy? Maybe. Intriguing? Indeed. 

Let's do more science with rocks!

Two impressive experiments, unabashedly and literally laid out for all to see, equipped with clever geologists, and enriched by supplementary technology. Both are thoughtful initiatives—real scientific experiments—that not only make the operating companies more profitable, but also profoundly improve our understanding of a precious resource for society. Two role models for how comprehensive experiments can serve more than just those who conduct them. Integration at its very best, centered on core.

What are the best examples of integrated geoscience that you've seen?

Submitting assumptions for meaningful answers

The best talk of the conference was Ran Bachrach's on seismics for unconventionals. He enthusiastically described the physics to his spectators with conviction and duty, and explained why they should care. Isotropic, VTI, and orthorhombic media anisotropy models are used not because they are right, but because they are simple. If the assumptions you bring to the problem are reasonable, the answers can be considered meaningful. If you haven't considered and tested your assumptions, you haven't subscribed to reason. In a sense, you haven't held up your end of the bargain, and there will never be agreement. This talk should be mandatory viewing for anyone working seismic for unconventionals. Advocacy for reason. Too bad it wasn't recorded.

I am both privileged and obliged to celebrate such nuggets of awesomeness. That's a big reason why I blog. And on the contrary, we should call out crappy talks when we see them to raise the bar. Indeed, to quote Zen Faulkes, "...we should start creating more of an expectation that scientific talks will be reviewed and critiqued. And names will be named."

The talk from HEF Petrophysical entitled, Towards modelling three-dimensional oil sands permeability distribution using borehole image logs, drew me in. I was curious enough to show up. But as the talk unfolded, my curiosity was left unsatisfied. A potentially interesting workflow of transforming high-resolution resistivity measurements into flow permeability was obfuscated with a pointless upscaling step. The meat of anything like this is in the transform itself, but it was missing. It's also the most trivial bit; just cross-plot one property with another and show people. So I am guessing they didn't have any permeability data. If that was the case, how can you stand up and talk about permeability? It was a sandwich without the filling. The essential thing that defines a piece of work is the creativity. The thing you add that wasn't there before. I was disappointed. Disappointed that it was accepted, and that no one else piped up. 

I will paraphrase a conversation I had with Ran at the coffee break: Some are not aware, some choose to ignore, and some forget that works of geoscience are problems of extreme complexity. In fact, the only way we can cope with complexity is to make certain assumptions that make our problem solvable. If all you do is say "here is my solution", you suck. But if instead you ask, "Have I convinced you that my assumptions are reasonable?", it entirely changes the conversation. It entirely changes the specialist's role. Only when you understand your assumptions can we talk about whether the results are reasonable. 

Have you ever felt conflicted on whether or not you should say something?

A really good conversation

Today was Day 2 of the Canada GeoConvention. But... all we had the energy for was the famous Unsolved Problems Unsession. So no real highlights today, just a report from the floor of Room 101.

Today was the day. We slept about as well as two 8-year-olds on Christmas Eve, having been up half the night obsessively micro-hacking our meeting design (right). The nervous anticipation was richly rewarded. About 50 of the most creative, inquisitive, daring geoscientists at the GeoConvention came to the Unsession — mostly on purpose. Together, the group surfaced over 100 pressing questions facing the upstream industry, then filtered this list to 4 wide-reaching problems of integration:

• making the industry more open
• coping with error and uncertainty
• improving seismic resolution
• improving the way our industry is perceived

We owe a massive debt of thanks to our heroic hosts: Greg Bennett, Tannis McCartney, Chris Chalcraft, Adrian Smith, Charlene Radons, Cale White, Jenson Tan, and Tooney Fink. Every one of them far exceeded their brief and brought 100× more clarity and continuity to the conversations than we could have had without them. Seriously awesome people.  

This process of waking our industry up to new ways of collaborating is just beginning. We will, you can be certain, write more about the unsession after we've had a little time to parse and digest what happened.

If you're at the conference, tell us what we missed today!

A revolution in seismic acquisition?

We're in warm, sunny Calgary for the GeoConvention 2013. The conference feels like it's really embracing geophysics this year — in the past it's always felt more geological somehow. Even the exhibition floor felt dominated by geophysics. Someone we spoke to speculated that companies were holding their geological cards close to their chests, but the service companies are still happy to talk about (ahem, promote) their geophysical advances.

Are you at the conference? What do you think? Let us know in the comments.

We caught about 15 talks of the 100 or so on offer today. A few of them ignited the old whines about half-cocked proofs of efficacy. Why is it still acceptable to say that a particular seismic volume or inversion result is 'higher resolution' or 'more geological' with nothing more than a couple of sections or timeslices as evidence?

People are excited about designing seismic acquisition expressly for wavefield reconstruction. In a whole session devoted to the subject, for example, Mauricio Sacchi showed how randomization helps with regularization in processing, allowing us to either get better image quality, or to lower cost. It feels like the start of a new wave of innovation in acquisition, which has more than its fair share of recent innovation: multi-component, wide azimuth, dual-sensor, simultaneous source...

Is it a revolution? Or just the fallacy of new things looking revolutionary... until the next new thing? It's intriguing to the non-specialist. People are talking about 'beyond Nyquist' again, but this time without inducing howls of derision. We just spent an hour talking about it, and we think there's something deep going on... we're just not sure how to articulate it yet.

Unsolved problems

We were at the conference today, but really we are focused on the session we're hosting tomorrow morning. Along with a roomful of adventurous conference-goers (you're invited too!), looking for the most pressing questions in subsurface science. We start at 8 a.m. in Telus 101/102 on the main floor of the north building.

What is an unsession?

Yesterday I invited you (yes, you) to our Unsolved Problems Unsession on 7 May in Calgary. What exactly will be involved? We think we can accomplish two things:

1. Brainstorm the top 10, or 20, or 50 most pressing problems in exploration geoscience today. Not limited to but focusing on those problems that affect how well we interface — with each other, with engineers, with financial people, with the public even. Integration problems.
2. Select one or two of those problems and solve them! Well, not solve them, but explore ways to approach solving them. What might a solution be worth? How many disciplines does it touch? How long might it take? Where could we start? Who can help?

There are bright, energetic young people out there looking for relevant problems to work on towards a Master's or PhD. There are entrepreneurs looking for high-value problems to create a new business from. And software companies looking for ways to be more useful and relevant to their users. And there is more than one interpreter wishing that innovation would speed up a bit in our industry and make their work a little — or a lot — easier. 

We don't know where it will lead, but we think this unsession is one way to get some conversations going. This is not a session to dip in and out of — we need 4 hours of your time. Bring your experience, your uniqueness, and your curiosity.

Let's reboot our imaginations about what we can do in our science.

An invitation to a brainstorm

Who of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries? What particular goals will there be toward which the leading [geoscientific] spirits of coming generations will strive? What new methods and new facts in the wide and rich field of [geoscientific] thought will the new centuries disclose?

— Adapted from David Hilbert (1902). Mathematical Problems, Bulletin of the American Mathematical Society 8 (10), p 437–479. Originally appeared in in Göttinger Nachrichten, 1900, pp. 253–297.

Back at the end of October, just before the SEG Annual Meeting, I did some whining about conferences: so many amazing, creative, energetic geoscientists, doing too much listening and not enough doing. The next day, I proposed some ways to make conferences for productive — for us as scientists, and for our science itself. 

Evan and I are chairing a new kind of session at the Calgary GeoConvention this year. What does ‘new kind of session’ mean? Here’s the lowdown:

The Unsolved Problems Unsession at the 2013 GeoConvention will transform conference attendees, normally little more than spectators, into active participants and collaborators. We are gathering 60 of the brightest, sparkiest minds in exploration geoscience to debate the open questions in our field, and create new approaches to solving them. The nearly 4-hour session will look, feel, and function unlike any other session at the conference. The outcome will be a list of real problems that affect our daily work as subsurface professionals — especially those in the hard-to-reach spots between our disciplines. Come and help shed some light, room 101, Tuesday 7 May, 8:00 till 11:45.

What you can do

• Where does your workflow stumble? Think up the most pressing unsolved problems in your workflows — especially ones that slow down collaboration between the disciplines. They might be organizational, they might be technological, they might be scientific.
• Put 7 May in your calendar and come to our session! Better yet, bring a friend. We can accommodate about 60 people. Be one of the first to experience a new kind of session!
• If you would like to help host the event, we're looking for 5 enthusiastic volunteers to play a slightly enlarged role, helping guide the brainstorming and capture the goodness. You know who you are. Email hello@agilegeoscience.com. 

Backwards and forwards reasoning

Most people, if you describe a train of events to them will tell you what the result will be. There will be few people however, that if you told them a result, would be able to evolve from their own consciousness what the steps were that led to that result. This is what I mean when I talk about reasoning backward.

— Sherlock Holmes, A Study in Scarlet, Sir Arthur Conan Doyle (1887)

Reasoning backwards is the process of solving an inverse problem — estimating a physical system from indirect data. Straight-up reasoning, which we call the forward problem, is a kind of data collection: empiricism. It obeys a natural causality by which we relate model parameters to the data that we observe.

Modeling a measurement

Where are you headed? Every subsurface problem can be expressed as the arrow between two or more such panels.Inverse problems exists for two reasons. We are incapable of measuring what we are actually interested in, and it is impossible to measure a subject in enough detail, and in all aspects that matter. If, for instance, I ask you to determine my weight, you will be troubled if the only tool I allow is a ruler. Even if you are incredibly accurate with your tool, at best, you can construct only an estimation of the desired quantity. This estimation of reality is what we call a model. The process of estimation is called inversion.

Measuring a model

Forward problems are ways in which we acquire information about natural phenomena. Given a model (me, say), it is easy to measure some property (my height, say) accurately and precisely. But given my height as the starting point, it is impossible to estimate the me from which it came. This is an example of an ill-posed problem. In this case, there is an infinite number of models that share my measurements, though each model is described by one exact solution. 

Solving forward problems are nessecary to determine if a model fits a set of observations. So you'd expect it to be performed as a routine compliment to interpretation; a way to validate our assumptions, and train our intuition.  

The math of reasoning

Forward and inverse problems can be cast in this seemingly simple equation.

where d is a vector containing N observations (the data), m is a vector of M model parameters (the model), and G is a N × M matrix operator that connects the two. The structure of G changes depending on the problem, but it is where 'the experiment' goes. Given a set of model parameters m, the forward problem is to predict the data d produced by the experiment. This is as simple as plugging values into a system of equations. The inverse problem is much more difficult: given a set of observations d, estimate the model parameters m.

I think interpreters should describe their work within the Gm = d framework. Doing so would safeguard against mixing up observations, which should be objective, and interpretations, which contain assumptions. Know the difference between m and d. Express it with an arrow on a diagram if you like, to make it clear which direction you are heading in.

Illustrations for this post were created using data from the Marmousi synthetic seismic data set. The blue seismic trace and its corresponding velocity profile is at location no. 250.

How to get paid big bucks

Yesterday I asked 'What is inversion?' and started looking at problems in geoscience as either forward problems or inverse problems. So what are some examples of inverse problems in geoscience? Reversing our forward problem examples:

• Given a suite of sedimentological observations, provide the depositional environment. This is a hard problem, because different environments can produce similar-looking facies. It is ill-conditioned, because small changes in the input (e.g. the presence of glaucony, or Cylindrichnus) produces large changes in the interpretation.
• Given a seismic trace, produce an impedance log. Without a wavelet, we cannot uniquely deduce the impedance log — there are infinitely many combinations of log and wavelet that will give rise to the same seismic trace. This is the challenge of seismic inversion. 

To solve these problems, we must use induction — a fancy name for informed guesswork. For example, we can use judgement about likely wavelets, or the expected geology, to constrain the geophysical problem and reduce the number of possibilities. This, as they say, is why we're paid the big bucks. Indeed, perhaps we can generalize: people who are paid big bucks are solving inverse problems...

• How do we balance the budget?
• What combination of chemicals might cure pancreatic cancer?
• What musical score would best complement this screenplay?
• How do I act to portray a grief-stricken war veteran who loves ballet?

What was the last inverse problem you solved?

Update on 2013-04-17 21:50 by Matt Hall

Moar inversion! Don't miss the previous post in this mini-series, or the next one — where things get a bit more mathy. 

What is inversion?

Inverse problems are at the heart of geoscience. But I only hear hardcore geophysicists talk about them. Maybe this is because they're hard problems to solve, requiring mathematical rigour and computational clout. But the language is useful, and the realization that some problems are just damn hard — unsolvable, even — is actually kind of liberating. 

Forwards first

Before worrying about inverse problems, it helps to understand what a forward problem is. A forward problem starts with plenty of inputs, and asks for a straightforward, algorithmic, computable output. For example:

• What is 4 × 5?
• Given a depositional environment, what sedimentological features do we expect?
• Given an impedance log and a wavelet, compute a synthetic seismogram.

These problems are solved by deductive reasoning, and have outcomes that are no less certain than the inputs.

Can you do it backwards?

You can guess what an inverse problem looks like. Computing 4 × 5 was pretty easy, even for a geophysicist, but it's not only difficult to do it backwards, it's impossible:

20 = what × what

You can solve it easily enough, but solutions are, to use the jargon, non-unique: 2 × 10, 7.2 × 1.666..., 6.3662 × π — you get the idea. One way to deal with such under-determined systems of equations is to know about, or guess, some constraints. For example, perhaps our system — our model — only includes integers. That narrows it down to three solutions. If we also know that the integers are less than 10, there can be only one solution.

Non-uniqueness is a characteristic of ill-posed problems. Ill-posedness is a dead giveaway of an inverse problem. Proposed by Jacques Hadamard, the concept is the opposite of well-posedness, which has three criteria:

• A solution exists.
• The solution is unique.
• The solution is well-conditioned, which means it doesn't change disproportionately when the input changes. 

Notice the way the example problem was presented: one equation, two unknowns. There is already a priori knowledge about the system: there are two numbers, and the operator is multiplication. In geoscience, since the earth is not a computer, we depend on such knowledge about the nature of the system — what the variables are, how they interact, etc. We are always working with a model of nature.

Tomorrow, I'll look at some specific examples of inverse problems, and Evan will continue the conversation next week.

Update on 2013-04-12 11:18 by Matt Hall

Don't miss the first follow-up to this article, How to get paid big bucks.