Get a telescope!
/In the recent How deep are the presents? post, I mentioned that I got a telescope this year — and I encouraged you to get one, because I kind of wish I’d got mine years ago. Since the observing conditions aren’t great tonight and I’m indoors anyway, I thought I’d elaborate a bit.
Not Hubble
The fun might not be obvious to all. Superficially, the experience is terrible — you read about some interesting object, noting its spectacular appearance in the obligatory Hubble photo, only to spend 45 minutes hunting for it before realizing it must be that dim grey smudge you tried to wipe off the eyepiece half an hour ago.
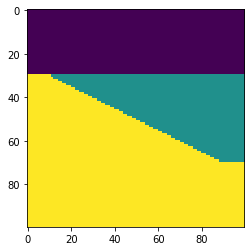
Messier 51: the Whirlpool Galaxy, which is actually a pair of colliding galaxies about 23 million light years away. What you’re expecting (left) vs what you might see on a really dark night with a lot of patience (right).
And yet… you did find it. Out in the dark, on your own, among the owls and foxes, you made an observation. You navigated to it, learning the names of ancient constellations and asterisms. You found out that it’s a pair of colliding galaxies 23 million light years away, and we know that because we can measure the light from individual stars they contain. Its photons were absorbed, after 23 million years oscillating through space, by your retinal cells. And maybe, just possibly, you glimpsed its archetypal spiral arms. And you ticked another Messier object off your list. Thirty minutes well spent! On to the next thing…
There are so many things to see
I knew it would be pretty cool to be able to see Saturn’s rings and the surface of the Moon, but a lot of things have been surprising to me:
Jupiter and Saturn are genuinely breathtaking. Seeing the moons of Jupter change continuously, or a shadow pass across its face, is remarkable — it’s the view that changed Galileo’s, then humanity’s, understanding of the universe, proving that Earth is not the centre of every celestial body’s orbit.
The moon looks different every day. This is obvious, of course, but with a decent telescope, you can see individual mountains and valleys pass from obscurity into high contrast, and then into blinding sunlight. The only trouble is that once it’s well-lit, the moonlight basically obliterates everything else.
Indeed, the whole sky changes continuously. Every month it advances two hours — so in January you can see at 8 pm what you had to wait until 10 pm for in December. So every month’s non-moonlit fortnight is different, with new constellations full of new objects appearing over the eastern horizon.
There’s a ready-made list of achievements for beginners to unlock, at least in the Northern Hemisphere. The objects on Charles Messier’s list of 110 “things that aren’t comets” are, because his late-18th-Century telescope was rubbish, fairly easy to observe — even from places that aren’t especially dark.
Many of the objects on that list are mind-blowingly cool. The colliding galaxies of M51 were the first thing I pointed my telescope at. M57, the famous Ring Nebula, is tiny but perfect and jewel-like. M42 is legitimately gasp-inducing. M13, the Great Globular Cluster, is extraordinarily bright and beautiful.
If you do start observing the night sky, I strongly recommend keeping a journal. You’ll quickly forget what you saw, and besides it’s fun to look back on all the things you’ve found. My own notes are pretty sketchy, as you can see below, but they have helped me learn the craft and I refer back to them quite often.
Buying a telescope
Telescopes are one of those purchases that can throw you into analysis paralysis, so I thought I’d share what I’ve learned as a noob stargazer.
Whatever you’re buying, buy from a telescope shop or online store that serves astronomers. If at all possible, don’t go to Amazon, a sporting goods store, or a department store.
If you’re spending under about $200, get the best binoculars you can find instead of a telescope. Look for aperture, not magnification (e.g. for 10 x 50 bins, 10 is the magnification, 50 is the aperture in mm). Just be aware that anything with an aperture greater than about 50 mm will start to get heavy and may need a tripod (and a binocular screw mount) to use effectively. Ideally, try some out in a shop.
Like lots of other things (groceries, bikes, empathy), telescopes are hard to find at the moment. So focus on what’s available — unless you are prepared to wait. There are good scopes available now, just maybe not that exact one you were looking for.
There are three basic kinds of optical telescope the beginner needs to know about: refractors, reflectors, and catadioptrics (a bit of both). I recommend going for a reflector, because big ones are cheap, and you can see more with a big scope. On the downside, they do get quite large and once you hit a 12-inch mirror, awkward to store, manoeuvre, and transport.
I know technology is cool, but if at all possible you should forget about fancy electronics, ‘go-to’ mounts, GPS-this, WiFi-that, and so on — for now. Relatedly, forget about anything to do with photographing the heavens. Unless you’ve been at it for a couple of years already (why are you reading this?), wait.
For your first scope, you’re looking for an alt-azimuth or Dobsonian mount, not an equatorial one. They aren’t ideal for taking photographs of anything other than very bright objects, but they are perfect for visual observation.
Don’t buy any extra doo-dads, except maybe a collimator (your scope will need aligning now and again), some sort of finder (red-dot finders are popular), and a moon filter (once its past first quarter, it’s too bright to look at). Everything else can wait. (Many scopes include these items though, so do check.)
I think that’s all the advice I’m entitled to offer at this point. But don’t just take it from me, here are some awesome “buying your first telescope” videos:
Trevor Jones is one of the superstars of backyard astronomy YouTube, and he knows what’s what.
Astrobiscuit always has good advice. His best ‘one scope’ is a Schmidt-Cassegrain, or SCT. I was very close to getting one of these, but in the end I opted to spend the dollar difference on aperture.
Ed Ting’s channel is a bit less energetic, but I think he offers solid advice, based on years of observing.
After much deliberation, I bought a Sky-Watcher Flextube 250P, which is a non-motorized, Dobsonian-mounted, 250-mm (10-inch) aperture Newtonian reflector. It’s been a delight, and I highly recommend it. If you decide to take the plunge, good luck! And do let me know how it goes.





































 Except where noted, this content is licensed
Except where noted, this content is licensed