Slicing seismic arrays
/Scientific computing is largely made up of doing linear algebra on matrices, and then visualizing those matrices for their patterns and signals. It's a fundamental concept, and there is no better example than a 3D seismic volume.
Seeing in geoscience, literally
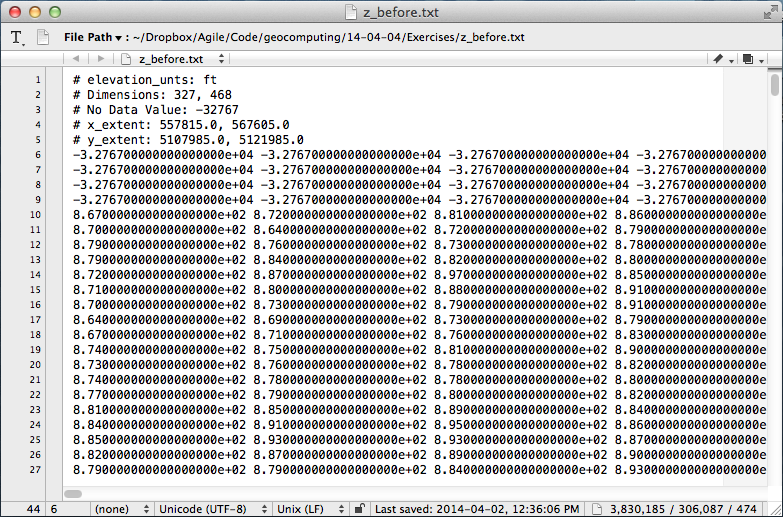
Digital seismic data is nothing but an array of numbers, decorated with header information, sorted and processed along different dimensions depending on the application.
In Python, you can index into any sequence, whether it be a string, list, or array of numbers. For example, we can index into the fourth character (counting from 0) of the word 'geoscience' to select the letter 's':
>>> word = 'geosciences'
>>> word[3]
's'
Or, we can slice the string with the syntax word[start:end:step] to produce a sub-sequence of characters. Note also how we can index backwards with negative numbers, or skip indices to use defaults:
>>> word[3:-1] # From the 4th character to the penultimate character.
'science'
>>> word[3::2] # Every other character from the 4th to the end.
'sine'
Seismic data is a matrix
In exactly the same way, we index into a multi-dimensional array in order to select a subset of elements. Slicing and indexing is a cinch using the numerical library NumPy for crunching numbers. Let's look at an example... if data is a 3D array of seismic amplitudes:
timeslice = data[:,:,122] # The 122nd element from the third dimension.
inline = data[30,:,:] # The 30th element from the first dimension.
crossline = data[:,60,:] # The 60th element from the second dimension.

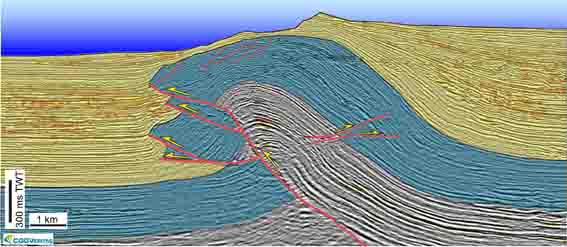
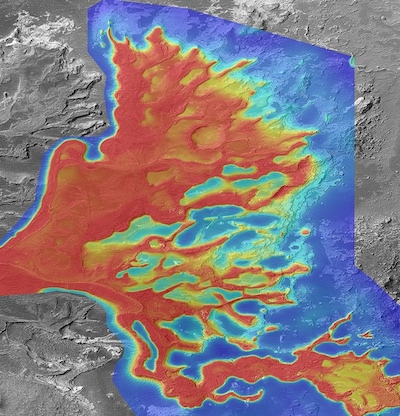
Here we have sliced all of the inlines and crosslines at a specific travel time index, to yield a time slice (left). We have sliced all the crossline traces along an inline (middle), and we have sliced the inline traces along a single crossline (right). There's no reason for the slices to remain orthogonal however, and we could, if we wished, index through the multi-dimensional array and extract an arbitrary combination of all three.
Questions involving well logs (a 1D matrix), cross sections (2D), and geomodels (3D) can all be addressed with the rigours of linear algebra and digital signal processing. An essential step in working with your data is treating it as arrays.
View the notebook for this example, or get the get the notebook from GitHub and play with around with the code.
Sign up!
If you want to practise slicing your data into bits, and other power tools you can make, the Agile Geocomputing course will be running twice in the UK this summer. Click one of the buttons below to buy a seat.
More locations in North America for the fall. If you would like us to bring the course to your organization, get in touch.




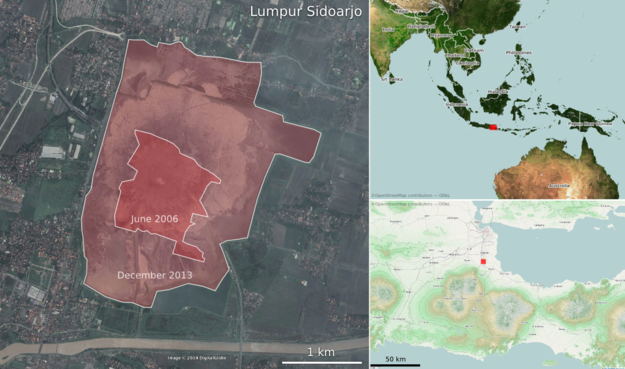

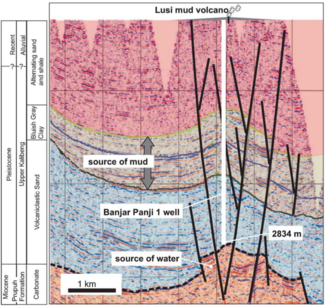
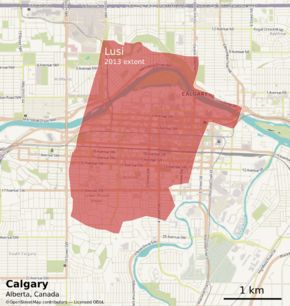
















 Except where noted, this content is licensed
Except where noted, this content is licensed